【题目】如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;② ![]() ;③PAPE=PBPC.其中,正确结论的个数为( )
;③PAPE=PBPC.其中,正确结论的个数为( ) 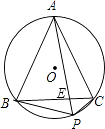
A.3个
B.2个
C.1个
D.0个
参考答案:
【答案】B
【解析】解:延长BP到D,使PD=PC,连接CD,可得∠CPD=∠BAC=60°, 则△PCD为等边三角形,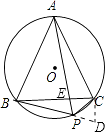
∵△ABC为正三角形,
∴BC=AC
∵∠PBC=∠CAP,∠CPA=∠CDB,
∴△APC≌△BDC(AAS).
∴PA=DB=PB+PD=PB+PC,故①正确;
由(1)知△PBE∽△PAC,则 ![]() ,
,
∴②错误;
∵∠CAP=∠EBP,∠BPE=∠CPA
∴△PBE∽△PAC
∴ ![]()
∴PAPE=PBPC,故③正确;
故选B.
根据题意:易得△APC≌△BDC.即AP=BD,有PA=DB=PB+PD=PB+PC正确.同时可得:②错误,同理易得△PBE∽△PAC,故有PAPE=PBPC;③正确.
-
科目: 来源: 题型:
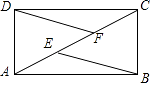
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
A.
B.1
C.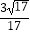
D.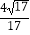
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )

A.1
B.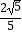
C.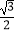
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数
 的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 .
的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
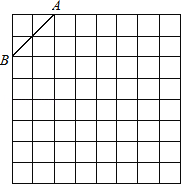
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
-
科目: 来源: 题型:
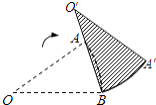
查看答案和解析>>【题目】如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π)
相关试题

