【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

参考答案:
【答案】解:(1)证明:∵四边形ABCD是菱形,∴AO=CO,AD∥BC。∴∠OAE=∠OCF。
![]() 在△AOE和△COF中,∵
在△AOE和△COF中,∵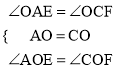 ,
,
∴△AOE≌△COF(ASA)。
(2)∵∠BAD=60°,∴∠DAO=![]() ∠BAD=
∠BAD=![]() ×60°=30°。
×60°=30°。
∵∠EOD=30°,∴∠AOE=90°﹣30°=60°。
∴∠AEF=180°﹣∠BOD﹣∠AOE=180°﹣30°﹣60°=90°。
∵菱形的边长为2,∠DAO=30°,∴OD=![]() AD=
AD=![]() ×2=1。
×2=1。
∴![]() 。
。
∴![]() 。
。
∵菱形的边长为2,∠BAD=60°,∴高![]() 。
。
在Rt△CEF中,  。
。
【解析】试题分析:(1)根据菱形的对角线互相平分可得AO=CO,对边平行可得AD∥BC,再利用两直线平行,内错角相等可得∠OAE=∠OCF,然后利用“角边角”证明△AOE和△COF全等。
(2)根据菱形的对角线平分一组对角求出∠DAO=30°,然后求出∠AEF=90°,然后求出AO的长,再求出EF的长,然后在Rt△CEF中,利用勾股定理列式计算即可得解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算|﹣4+1|的结果是( )
A.﹣5
B.﹣3
C.3
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2+ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的周长比为1:3,则它们的面积比为( )
A.1:9B.1:6C.1:3D.6:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.
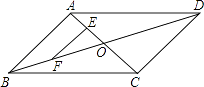
-
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘2018年初房价为每平方米20000元,经过两年连续降价后,2020 年初房价为16200元。设该楼盘这两年房价年平均降低的百分率为x,根据题意可列方程为__________.
相关试题

