搜索
【题目】如图1，⊙O过正方形ABCD的顶点A、D且与边BC相切于点E，分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x，圆心O与P点的距离为y，图2记录了一段时间里y与x的函数关系，在这段时间里P点的运动路径为（ ）
A. 从D点出发，沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发，沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发，沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发，沿线段CN→弧ND→弧DA→线段AB
参考答案：
【答案】C
【解析】结合两幅图形分析可知，图2中函数图象的线段部分对应的是点P在⊙O上运动的情形，曲线部分对应的是点P在正方形的边上运动的情形，在图2中函数图象的最高点分别对应着点P运动到了图1中的B、C两点， 由此可知与图2中函数图象对应的点P的运动路线有以下两种情况：①点P是从A点出发，沿弧AM→线段BM→线段BC→线段CN：②点P是从D点出发，沿弧DN→线段NC→线段CB→线段BM.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有30箱苹果，以每箱20千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质质量的差
（单位：千克）
1
2
箱数
2
6
10
8
4
（1）这30箱苹果中，最重的一箱比最轻的一箱重多少千克？
（2）与标准质量比较，这30箱苹果总计超过或不足多少千克？
（3）若苹果每千克售价6元，则出售这30箱苹果可卖多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校科技实践社团制作实践设备，小明的操作过程如下：
①小明取出老师提供的圆形细铁环，先通过在圆一章中学到的知识找到圆心O，再任意找出圆O的一条直径标记为AB（如图1），测量出AB=4分米；
②将圆环进行翻折使点B落在圆心O的位置，翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D（如图2）；
③用一细橡胶棒连接C、D两点（如图3）；
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为（ ）
A. 2
分米 B. 2
分米 C. 3
分米 D. 3
分米 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：
，
．（1）求B；(用含a、b的代数式表示)
（2）比较A与B的大小．
-
科目： 来源： 题型：
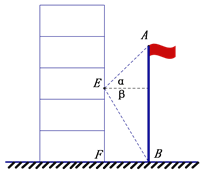
查看答案和解析>>【题目】数学实践课上，同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案，然后开始测量了.他们全组分成两个测量队，分别负责室内测量和室外测量（如图）.室内测量组来到教室内窗台旁，在点E处测得旗杆顶部A的仰角α为45°，旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
在数学课上，老师提出利用尺规作图完成下面问题：
已知：△OAB.
求作：⊙O，使⊙O与△OAB的边AB相切.
小明的作法如下：
如图，①取线段OB的中点M；以M为圆心，MO为半径作⊙M，与边AB交于点C；
②以O为圆心，OC为半径作⊙O；
所以，⊙O就是所求作的圆.
请回答：这样做的依据是__________________________________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），交y轴于点A（0，a），且a、p满足
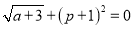．（1）求直线AP的解析式；
（2）如图1，点P关于y轴的对称点为Q，R（0，2），点S在直线AQ上，且SR=SA，求直线RS的解析式和点S的坐标；
（3）如图2，点B（﹣2，b）为直线AP上一点，以AB为斜边作等腰直角三角形ABC，点C在第一象限，D为线段OP上一动点，连接DC，以DC为直角边，点D为直角顶点作等腰三角形DCE，EF⊥x轴，F为垂足，下列结论：①2DP+EF的值不变；②
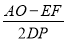的值不变；其中只有一个结论正确，请你选择出正确的结论，并求出其定值．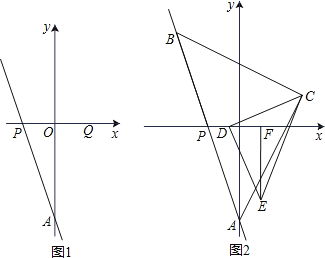
相关试题
