【题目】如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a﹣2b)2+|a+b﹣5|=0. 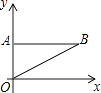
(1)求点B的坐标并求△AOB的面积S△AOB;
(2)在x轴上是否存在一点D,使得S△AOB=2S△AOD?若存在,求出D点的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)解:∵(3a﹣2b)2+|a+b﹣5|=0,
∴ ![]() ,
,
解得: ![]() ,
,
∴B(3,2);
S△AOB= ![]() ×2×(3﹣0)=3
×2×(3﹣0)=3
(2)解:设D(x,0),
∵S△AOB=2S△AOD,
∴2× ![]() ×2|x|=3,
×2|x|=3,
解得:x=﹣ ![]() ,或
,或 ![]() ,
,
D为(﹣ ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)根据非负数的性质求得a,b即可;(2)设D(x,0),根据S△AOB=2S△AOD即可求得x的长,进而求得D的坐标.
【考点精析】通过灵活运用三角形的面积和坐标与图形变化-平移,掌握三角形的面积=1/2×底×高;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
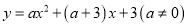 与
与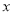 轴交于点A(4,0),与
轴交于点A(4,0),与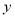 轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作
轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作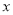 轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求
 的值和直线AB的函数表达式;
的值和直线AB的函数表达式;(2)在P点运动的过程中,请用含m的代数式表示线段PN;
(3)设△PMN的周长为
 ,△AEN的周长为
,△AEN的周长为 ,若
,若 ,求m的值;
,求m的值;(4)如图2,在(3)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接
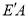 、
、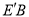 ,求
,求 的最小值.
的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
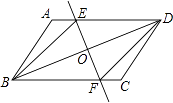
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+k﹣1=0有两个不相等的实数根,则实数k的取值范围是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(6a3b4)÷(3a2b)=( )
A. 2 B. 2ab3 C. 3ab3 D. 2a5b5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=
 ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
相关试题

