【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
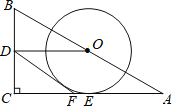
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF![]() 时,求⊙O的半径.
时,求⊙O的半径.
参考答案:
【答案】(1)结论:DF是⊙O的切线.理由见解析;(2)OE=1.
【解析】
(1)结论:DF是⊙O的切线.作OG⊥DF于G.连接OE.想办法证明OG=OE即可解决问题;
(2)由FA,FD是⊙O的切线,推出FG=FE,设FG=FE=x,由△OGD≌△DCF(AAS),推出DG=CF=![]() ,推出OD=DF=
,推出OD=DF=![]() +x,由AC=2OD,CE=OD,推出AE=EC=OD=
+x,由AC=2OD,CE=OD,推出AE=EC=OD=![]() +x,由∠A=30°,推出CD=OE=
+x,由∠A=30°,推出CD=OE=![]() ,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题;
,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题;
(1)结论:DF是⊙O的切线.
理由:作OG⊥DF于G.连接OE.
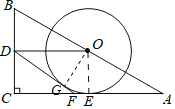
∵BD=DC,BO=OA,
∴OD∥AC,
∴∠ODG=∠DFC,
∵∠OGD=∠DCF=90°,OD=DF,
∴△OGD≌△DCF(AAS),
∴OG=CD,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠AEO=∠C=90°,
∴OE∥BC,
∵OD∥CD,
∴四边形CDOE是平行四边形,
∴CD=OE,
∴OG=OE,
∴DF是⊙O的切线.
(2)∵FA,FD是⊙O的切线,
∴FG=FE,设FG=FE=x,
∵△OGD≌△DCF(AAS),
∴DG=CF=![]() ,
,
∴OD=DF=![]() +x,
+x,
∵AC=2OD,CE=OD,
∴AE=EC=OD=![]() +x,
+x,
∵∠A=30°,
∴CD=OE=![]() ,
,
在Rt△DCF中,∵DF2=CD2+CF2,
∴(![]() +x)2=(
+x)2=(![]() )2+(
)2+(![]() )2,
)2,
解得x=![]() -
-![]() 或-
或-![]() -
-![]() (舍弃),
(舍弃),
∴OE=![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
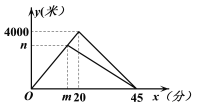
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A1,A2,A3…,An,An+1是直线
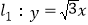 上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线
上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线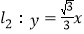 相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)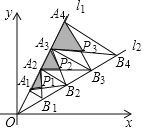
-
科目: 来源: 题型:
查看答案和解析>>【题目】某报刊销售处从报社购进甲、乙两种报纸进行销售.已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、1.5元.销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问该销售处每天最多购进甲种报纸多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,AB=1,点C的坐标为(6,2),E是AD的中点;反比例函数y1=
 (x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.(1)求反比例函数的解析式和点E的坐标;
(2)求直线BF的解析式;
(3)直接写出y1>y2时,自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,
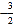 ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.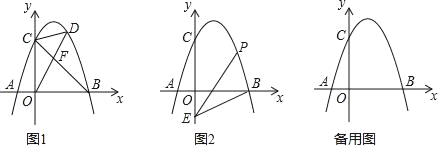
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

