【题目】如图,A1,A2,A3…,An,An+1是直线![]() 上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线
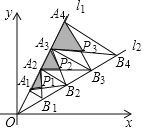
上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线![]() 相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
参考答案:
【答案】![]()
![]()
【解析】
设△OA1B1的面积为S.由OA1=A1A2=A2A3=…AnAn+1,A1B1∥A2B2∥A3B3∥…∥AnBn,推出A1B1:A2B2:A3B3:…:AnBn=1:2:3:…:n,推出![]() =S,
=S,![]() =2S,…,
=2S,…,![]() =nS,探究规律,利用规律即可解决问题;
=nS,探究规律,利用规律即可解决问题;
设△OA1B1的面积为S.
由题意可知OA1=A1A2=A2A3=…AnAn+1,A1B1∥A2B2∥A3B3∥…∥AnBn,
∴A1B1:A2B2:A3B3:…:AnBn=1:2:3:…:n,
∴![]() =S,
=S,![]() =2S,…,
=2S,…,![]() =nS,
=nS,
∴S1=![]() S,S2=
S,S2=![]() 2S,S3=
2S,S3=![]() 3S,…,Sn=
3S,…,Sn=![]() nS,
nS,
∵直线![]() 上的点,直线
上的点,直线![]() ,
,
∴两条直线与x轴的夹角分别为60°和30°,
∴∠A1OB1=30°,
∵OA1=2,
∴A1B1=![]()
∴S=![]()
∴Sn=![]()
![]() ,
,
故答案为:![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

-
科目: 来源: 题型:
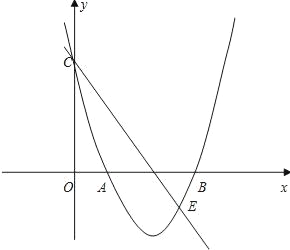
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求这个二次函数的解析式;
(2)过点C的直线y=kx+b与这个二次函数的图象相交于点E(4,m),请求出△CBE的面积S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
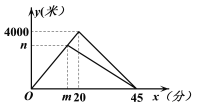
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某报刊销售处从报社购进甲、乙两种报纸进行销售.已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、1.5元.销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问该销售处每天最多购进甲种报纸多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
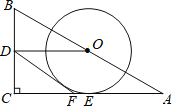
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF
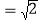 时,求⊙O的半径.
时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,AB=1,点C的坐标为(6,2),E是AD的中点;反比例函数y1=
 (x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.(1)求反比例函数的解析式和点E的坐标;
(2)求直线BF的解析式;
(3)直接写出y1>y2时,自变量x的取值范围.

相关试题

