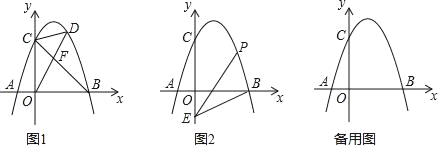
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣x2+2x+3;(2)点D的坐标为(1,4)或(2,3);(3)点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)OB=OC=3,则:B(3,0),C(0,-3),把B、C坐标代入抛物线方程,解得抛物线方程为:y=-x2+2x+3;
(2)S△COF:S△CDF=3:2,则S△COF=![]() S△COD,即:xD=
S△COD,即:xD=![]() xF,即可求解;
xF,即可求解;
(3)分∠PBE或∠PEB等于2∠OBE两种情况分别求解即可.
(1)OB=OC=3,则:B(3,0),C(0,﹣3),
把B、C坐标代入抛物线方程,
解得抛物线方程为:y=﹣x2+2x+3;
(2)∵S△COF:S△CDF=3:2,
∴S△COF=![]() S△COD,即:xD=
S△COD,即:xD=![]() xF,
xF,
设:F点横坐标为3t,则D点横坐标为5t,
点F在直线BC上,
而BC所在的直线方程为:y=﹣x+3,则F(3t,3﹣3t),
则:直线OF所在的直线方程为:y=![]() x=
x=![]() x,
x,
则点D(5t,5﹣5t),
把D点坐标代入①,解得:t=![]() 或
或![]() ,
,
则点D的坐标为(1,4)或(2,3);
(3)①如图所示,当∠PEB=2∠OBE=2α时,
过点E作∠PEB的平分线交x轴于G点,PE交x轴于H点,
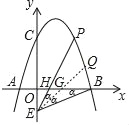
则:∠PEQ=∠QEB=∠ABE=α,则∠HGE=2α,
设:GB=m,则:OG=3﹣m,GE=m,
在Rt△OGE中,由勾股定理得:EG2=OG2+OE2,
即:m2=(3﹣m)2+(![]() )2,解得:m=
)2,解得:m=![]() ,
,
则:GE=![]() ,OG=
,OG=![]() ,BE=
,BE=![]() ,
,
∵∠PEQ=∠ABE=α,∠EHG=∠EHG,∴△HGE∽△HEB,
∴![]() =
=![]() =
=![]() ,设:GH=
,设:GH=![]() x,HE=4x,
x,HE=4x,
在Rt△OHE中,OH=OG﹣HG=![]() ﹣
﹣![]() x,OE=
x,OE=![]() ,EH=4x,
,EH=4x,
由勾股定理解得:x=![]() ,则:OH=
,则:OH=![]() ,H(
,H(![]() ,0),
,0),
把E、H两点坐标代入一次函数表达式,
解得EH所在直线的表达式为:y=![]() x﹣
x﹣![]() ,
,
将上式与①联立并解得:x=![]() ,
,
则点P(![]() ,
,![]() );
);
②当∠PBE=2∠OBE时,则∠PBO=∠EBO,
BE所在直线的k值为![]() ,则BE所在直线的k值为﹣
,则BE所在直线的k值为﹣![]() ,
,
则:PB所在的直线方程为:y=﹣![]() x+3,
x+3,
将上式与①联立,解得:x=![]() ,(x=0已舍去),
,(x=0已舍去),
则点P(![]() ,
,![]() ),
),
故:点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某报刊销售处从报社购进甲、乙两种报纸进行销售.已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、1.5元.销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问该销售处每天最多购进甲种报纸多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
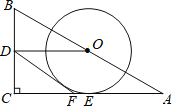
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF
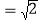 时,求⊙O的半径.
时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD在平面直角坐标系的第一象限内,BC与x轴平行,AB=1,点C的坐标为(6,2),E是AD的中点;反比例函数y1=
 (x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.
(x>0)图象经过点C和点E,过点B的直线y2=ax+b与反比例函数图象交于点F,点F的纵坐标为4.(1)求反比例函数的解析式和点E的坐标;
(2)求直线BF的解析式;
(3)直接写出y1>y2时,自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
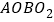 的顶点
的顶点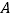 的坐标为
的坐标为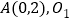 为正方形
为正方形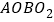 的中心;以正方形
的中心;以正方形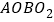 的对角线
的对角线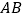 为边,在
为边,在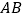 的右侧作正方形
的右侧作正方形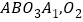 为正方形
为正方形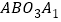 的中心;再以正方形
的中心;再以正方形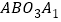 的对角线
的对角线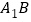 为边,在
为边,在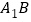 的右侧作正方形
的右侧作正方形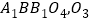 为正方形
为正方形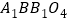 的中心;再以正方形
的中心;再以正方形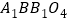 的对角线
的对角线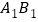 为边,在
为边,在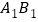 的右侧作正方形
的右侧作正方形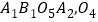 为正方形
为正方形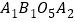 的中心:…;按照此规律继续下去,则点
的中心:…;按照此规律继续下去,则点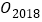 的坐标为_____.
的坐标为_____.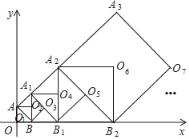
-
科目: 来源: 题型:
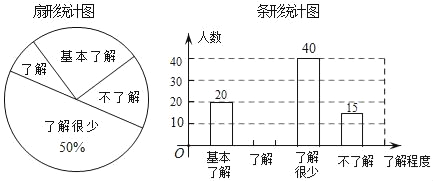
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调査的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 °;
(2)请补全条形统计图;
(3)若该中学共有学生1600人,请根据上述调查结果,估计该学校学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
相关试题

