【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
参考答案:
【答案】(1)见解析;(2)存在.整数k的值为±4.(3)EF的最大值是4.
【解析】
(1)先求出二次函数y=ax2﹣2ax=a(x﹣1)2﹣a顶点C(1,﹣a),当x=1时,一次函数值y=﹣a所以点C在一次函数y=﹣ax的图象上;
(2)存在.将点(k,y1)、(k+2,y2)(k≠0,±2)代入二次函数解析式,用a、k表示出y1、y2,因为满足![]() ,把y1、y2代入整理可得关于k的方程,解方程检验即可求得k的值.
,把y1、y2代入整理可得关于k的方程,解方程检验即可求得k的值.
(3)分两种情况讨论:①当﹣1≤n≤0时,EF=yE﹣yF=an2﹣2an﹣(﹣an)=![]() ②当0<n≤1时,EF=yF﹣yE=﹣an﹣(an2﹣2an)=
②当0<n≤1时,EF=yF﹣yE=﹣an﹣(an2﹣2an)=![]()
(1)∵二次函数y=ax2﹣2ax=a(x﹣1)2﹣a,
∴顶点C(1,﹣a),
∵当x=1时,一次函数值y=﹣a
∴点C在一次函数y=﹣ax的图象上;
(2)存在.
∵点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,
∴y1=ak2﹣2ak,y2=a(k+2)2﹣2a(k+2),
∵满足![]()
∴![]() ,
,
整理,得 ![]() ,
,
∴![]()
∴![]() ,
,
解得k=±4,
经检验:k=±4是原方程的根,
∴整数k的值为±4.
(3)∵点E是二次函数图象上一动点,
∴E(n,an2﹣2an),
∵EF∥y轴,F在一次函数图象上,∴F(n,﹣an).
①当﹣1≤n≤0时,EF=yE﹣yF=an2﹣2an﹣(﹣an)=![]()
∵a>0,
∴当n=﹣1时,EF有最大值,且最大值是2a,
又∵0<a≤2,
∴0<2a≤4,即EF的最大值是4;
②当0<n≤1时,EF=yF﹣yE=﹣an﹣(an2﹣2an)=![]() 此时EF的最大值是
此时EF的最大值是![]() ,
,
又∵0<a≤2,
∴0<![]() ≤
≤![]() ,即EF的最大值是
,即EF的最大值是![]() ;
;
综上所述,EF的最大值是4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件)
生产乙种产品数(件)
所用时间(分钟)
10
10
350
30
20
850
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 的边长为1,点
的边长为1,点 是
是 边上的一个动点(与
边上的一个动点(与 ,
, 不重合),以
不重合),以 为顶点在
为顶点在 所在直线的上方作
所在直线的上方作
(1)当
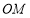 经过点
经过点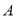 时,
时,①请直接填空:
 ________(可能,不可能)过
________(可能,不可能)过 点:(图1仅供分析)
点:(图1仅供分析)②如图2,在
 上截取
上截取 ,过
,过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,作
,作 于
于 ,求证:四边形
,求证:四边形 为正方形;
为正方形;③如图2,将②中的已知与结论互换,即在
 上取点
上取点 (
( 点在正方形
点在正方形 外部),过
外部),过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,作
,作 于
于 ,若四边形
,若四边形 为正方形,那么
为正方形,那么 与
与 是否相等?请说明理由;
是否相等?请说明理由;(2)当点
 在射线
在射线 上且
上且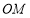 不过点
不过点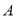 时,设
时,设 交边
交边 于
于 ,且
,且 .在
.在 上存在点
上存在点 ,过
,过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,使得
,使得 ,连接
,连接 ,则当
,则当 为何值时,四边形
为何值时,四边形 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加“仙桃市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(l)班 86,85,77,92,85;八(2)班 79,85,92,85,89.通过数据分析,列表如下:
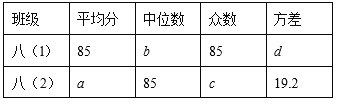
(1)直接写出表中a,b,c,d的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=-
 ,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=
 x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

