【题目】已知:如图,梯形ABCD中,AD∥BC,∠B=90°,AD=AB=4,BC=7,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点C'处.
(1)求∠C'DE的度数;
(2)求△C'DE的面积.

参考答案:
【答案】(1)45°;(2)![]() .
.
【解析】
(1)首先作DF⊥BC于F,根据已知证出△AC′D≌△FCD,再求出∠C′DE=∠CDE,即可得出答案;(2)根据EC=x,则BE=7-x,C′E=x,再根据勾股定理求出EC的长,即可求出△C′DE的面积.
(1)过点D作DF⊥BC于F
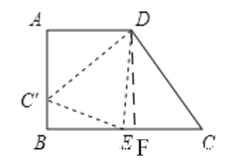
∵AD∥BC,∠B=90°,AD=AB,
∴四边形ABFD是正方形.
∴DF=BF=AB=4,FC=3,
在Rt△DFC中,
![]() ,
,
∴C′D=5,
∵AD=FD,∠A=∠DFC=90°,C′D=CD,
∴△AC′D≌△FCD,
∴∠ADC′=∠FDC,AC′=FC=3,
∴∠ADF=∠ADC′+∠C′DF=∠FDC+∠C′DF=∠C′DC=90°,
∵∠C′DE=∠CDE,
∴∠C′DE=45°;
(2)设EC=x,则BE=7-x,C′E=x,
∵AC′=3,
∴BC'=1,
在Rt△BEC′中(7-x)2+1=x2
解方程,得:![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,Rt△ABC中,∠ACB=90°,D为AB中点,DE、DF分别交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA<CB,(1)中结论还能成立吗?若成立,请证明;若不成立,请说明理由.
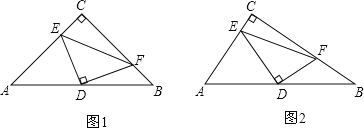
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上.
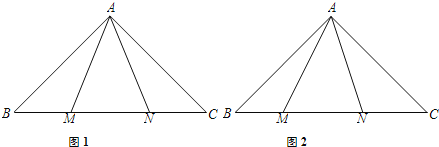
(1)如图1,如果AM=AN,求证:BM=CN;
(2)如图2,如果M、N是边BC上任意两点,并满足∠MAN=45°,那么线段BM、MN、NC是否有可能使等式MN2=BM2+NC2成立?如果成立,请证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是
A.3a+2b=5ab
B.(-3a2b)2=-6a4b2
C. +
+  =4
=4 
D.(a-b)2=a2-b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】西瓜和甜瓜是新疆特色水果,小明的妈妈先购买了2千克西瓜和3千克甜瓜,共花费9元;后又购买了1千克西瓜和2千克甜瓜,共花费5.5元.(每次两种水果的售价都不变)
(1)求两种水果的售价分别是每千克多少元?
(2)如果还需购买两种水果共12千克,要求甜瓜的数量不少于西瓜数量的两倍,请设计一种购买方案,使所需总费用最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点A、C分别在直线a、b上,且a∥b , ∠1=65°,则∠2的度数为
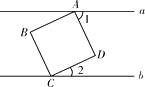
A.65°
B.55°
C.35°
D.25° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.

(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
相关试题

