【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD. 
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
参考答案:
【答案】
(1)解:四边形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)解:连接OE.

由菱形OCED得:CD⊥OE,
又∵BC⊥CD,
∴OE∥BC(在同一平面内,垂直于同一条直线的两直线平行),
又∵CE∥BD,
∴四边形BCEO是平行四边形;
∴OE=BC=8
∴S四边形OCED= ![]() OECD=
OECD= ![]() ×8×6=24.
×8×6=24.
【解析】(1)首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.(2)连接OE,通过证四边形BOEC是平行四边形,得OE=BC;根据菱形的面积是对角线乘积的一半,可求得四边形ODEC的面积.
【考点精析】关于本题考查的平行四边形的判定和菱形的判定方法,需要了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)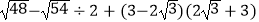
(2)(3 ﹣2
﹣2  +
+  )÷2
)÷2 
(3)先化简,再求值: 其中a=
其中a=  +1.
+1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AB的长为2a,点P是AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD.
(1)当△APC与△PBD的面积之和取最小值时,AP=_______;(直接写结果)
(2)连接AD、BC,相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动面变化?请说明理由;
(3)如图2,若点P固定,将△PBD绕点P按顺时针方向旋转(旋转角小于180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“对顶角相等”这个命题的逆命题是____________________,它是一个________命题(填“真”或“假”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程ax2+2x﹣1=0有两个实数根,则a的取值范围是( )
A. a≤1B. a≥﹣1且a≠0C. a>1且a≠0D. a≥﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,求DN+MN的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a3﹣16a=_____.
相关试题

