【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
参考答案:
【答案】C
【解析】
在Rt△ABC中利用勾股定理可求出AC=10,设BE=a,则CE=8﹣a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=4,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8﹣a中即可得出线段CE的长度.
解:在Rt△ABC中,AB=6,BC=8,
∴AC=10.
设BE=a,则CE=8﹣a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=4.
在Rt△CEF中,EF=a,CE=8﹣a,CF=4,
∴CE2=EF2+CF2,即(8﹣a)2=a2+42,
解得:a=3,
∴8﹣a=5.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣2|+( )﹣1﹣(
)﹣1﹣(  ﹣2010)0﹣
﹣2010)0﹣  tan60°
tan60°
(2)先化简,再求值: ÷(x﹣
÷(x﹣  ),其中x=
),其中x=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将△ABC纸片沿DE折叠,使点C落在四边形ABDE内点C’的位置,
(1)①若
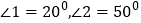 ,则
,则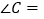 ;
;②若
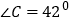 ,则
,则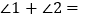 ;
;③探索
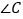 、
、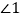 与
与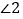 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;(2)直接按照所得结论,填空:
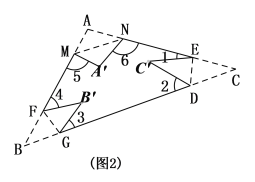
①如图中,将△ABC纸片再沿FG、MN折叠,使点A、B分别落在△ABC内点A’、B’的位置,则
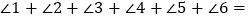 ;
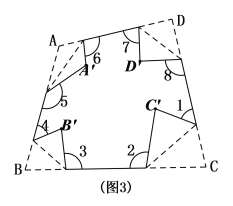
;②如图中,将四边形ABCD按照上面方式折叠,则
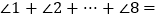 ;
;③若将n边形
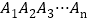 也按照上面方式折叠,则
也按照上面方式折叠,则 ;
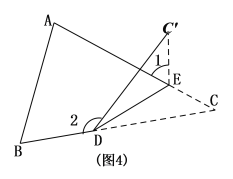
;(3)如图,将△ABC纸片沿DE折叠,使点
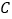 落在△ABC边
落在△ABC边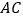 上方点
上方点 的位置, 探索
的位置, 探索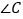 、
、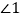 与
与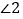 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.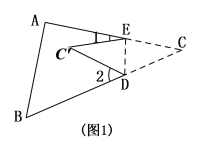
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC=
 ∠BAC.
∠BAC.
其中正确的结论有( )
A. 5个 B. 4个
C. 3个 D. 2个
相关试题

