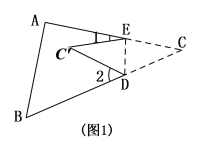
【题目】如图1,将△ABC纸片沿DE折叠,使点C落在四边形ABDE内点C’的位置,
(1)①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)直接按照所得结论,填空:
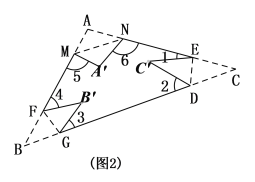
①如图中,将△ABC纸片再沿FG、MN折叠,使点A、B分别落在△ABC内点A’、B’的位置,则![]() ;
;
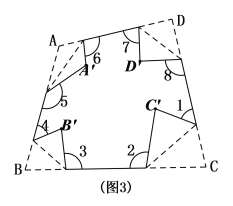
②如图中,将四边形ABCD按照上面方式折叠,则![]() ;
;
③若将n边形![]() 也按照上面方式折叠,则
也按照上面方式折叠,则![]() ;
;
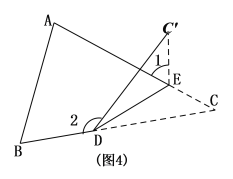
(3)如图,将△ABC纸片沿DE折叠,使点![]() 落在△ABC边
落在△ABC边![]() 上方点
上方点![]() 的位置, 探索
的位置, 探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;③
;③![]() ;(2)①
;(2)①![]() ;②
;②![]() ;③
;③![]() ;(3)
;(3)![]()
【解析】
(1)①由邻补角的定义可知∠CEC′=160°,∠CDC′=130°,根据折叠的性质可求出∠CED=80°,∠CDE=65°,然后根据三角形内角和定理求解即可;
②由三角形内角和可求出∠CED+∠CDE=138°,再由折叠的性质可知∠CEC′+∠CDC′=276°,然后根据邻补角的定义可求出![]() 84°;
84°;
③由邻补角定义可知![]() ,从而
,从而![]() ,所以,∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °,结合
,所以,∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °,结合![]() ,可求出
,可求出![]() ;
;
(2)① 由(1)得![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,从而
2∠A,从而![]() 2(∠A+∠B +∠C),结合三角形内角和求解即可;
2(∠A+∠B +∠C),结合三角形内角和求解即可;
②由①可知,![]() 2(∠A+∠B +∠C+∠D),结合四边形内角和求解即可;
2(∠A+∠B +∠C+∠D),结合四边形内角和求解即可;
③由①可知,![]() ;
;
(3)由外角的性质可知∠2=∠3+∠C,∠3=∠1+∠C,整理可得![]() .
.
解:(1)①∵![]() ,
,
∴∠CEC′=160°,∠CDC′=130°,
∵ ∠CED=80°,∠CDE=65°,
∴∠C= 180°-80°-65°=35°;
②∵
∴ ∠CED+∠CDE=180°-42°=138°,
∴∠CEC′+∠CDC′=276°,
∴![]() 360°-276°=84°;
360°-276°=84°;
③![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
因为在四边形![]() 中,
中,![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() .
.
(2)① 由①得
![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,
2∠A,
∴![]() 2(∠A+∠B +∠C)=360°;
2(∠A+∠B +∠C)=360°;
②∵![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,
2∠A,![]() 2∠D,
2∠D,
∴![]() 2(∠A+∠B +∠C+∠D)=2×360°=720°;
2(∠A+∠B +∠C+∠D)=2×360°=720°;
③∵n边形内角和是![]() ,
,
∴![]() ;
;
(3)![]() .
.
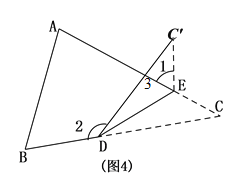
∵∠2=∠3+∠C,
∠3=∠1+∠![]() =∠1+∠C,
=∠1+∠C,
∴∠2=∠1+∠C +∠C=∠1+2∠C,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC=
 ∠BAC.
∠BAC.
其中正确的结论有( )
A. 5个 B. 4个
C. 3个 D. 2个
-
科目: 来源: 题型:
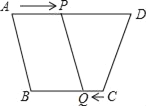
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=8cm,P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,_____秒后四边形ABQP是平行四边形.
相关试题

