【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.
∠BAC.
其中正确的结论有( )

A. 5个 B. 4个
C. 3个 D. 2个
参考答案:
【答案】B
【解析】(1)∵AD平分△ABC的外角∠EAC
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确。
(2)由(1)可知AD∥BC
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确。
(3)在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正确,
(4)如果BD平分∠ADC,则四边形ABCD是平行四边形,
∵∠ABD=∠ADB,
∴AB=AD,
∴四边形ABCD是菱形,
∴只有在△ABC是正三角形时才有BD平分∠ADC
故④错误。
(5)∵∠BAC+∠ABC=∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=
∠ABC=![]() ∠ACF,
∠ACF,
∵∠BDC+∠DBC=![]() ∠ACF,
∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=∠BDC+∠DBC,
∠ABC=∠BDC+∠DBC,
∵∠DBC=![]() ∠ABC,
∠ABC,
∴![]() ∠BAC=∠BDC,即∠BDC=
∠BAC=∠BDC,即∠BDC=![]() ∠BAC.
∠BAC.
故⑤正确。
故答案为:①②③⑤。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年某市政府投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
A. 2(1+x)2=9.5 B. 2(1+x)+2(1+x)2=9.5
C. 2+2(1+x)+2(1+x)2=9.5 D. 8+8(1+x)+8(1+x)2=9.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
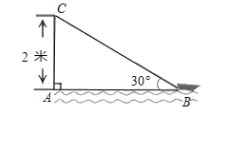
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图是一个数值运算程序,当输入值为-2时,则输出的数值为_____________

A. 3 B. 8 C. 64 D. 63
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC三个项点坐标分别为 A(3,2)、B(0,2)、C(0,5),将三角形ABC沿 y 轴正方向平移2个单位,再沿x轴负方向平移 l 个单位,得到三角形A1B1C1.

(1)画出三角形A1B1C1,并分别写出三个顶点的坐标;
(2)求三角形的面积A1B1C1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车在下午13点从停车场出发,沿着东西向的大街行驶,到下午15点的行驶记录如下:(向东行驶记为正,向西行驶记为负,单位:千米)-4、+7、-9、+8、+6、-4、-3、+12
(1)下午15点,出租车在什么位置?
(2)若汽车每千米耗油0.2升,则下午13点到下午15点,出租车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
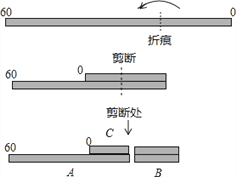
A. 20 B. 25 C. 30 D. 35
相关试题

