【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 、
、![]() 在坐标轴上,
在坐标轴上, ![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,点
得到的,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,平面内是否存在点
轴上,平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请直接写出点
为顶点的四边形是矩形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)可求得![]() 、
、![]() 的坐标,利用待定系数法可求得直线
的坐标,利用待定系数法可求得直线![]() 的解析式;
的解析式;
(2)可求得![]() 点坐标,求出直线
点坐标,求出直线![]() 的解析式,联立直线
的解析式,联立直线![]() 、
、![]() 解析式可求得
解析式可求得![]() 点的横坐标,可求得
点的横坐标,可求得![]() 的面积;
的面积;
(3)当![]() 为直角三角形时,可找到满足条件的点
为直角三角形时,可找到满足条件的点![]() ,分
,分![]() 、
、![]() 和
和![]() 三种情况,分别求得
三种情况,分别求得![]() 点的坐标,可分别求得矩形对角线的交点坐标,再利用中点坐标公式可求得
点的坐标,可分别求得矩形对角线的交点坐标,再利用中点坐标公式可求得![]() 点坐标.
点坐标.
解:(1)![]() ,
,![]() ,
,
![]() ,
,
![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,
得到的,
![]() ,
,![]() ,
,
![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 、
、![]() 坐标代入可得
坐标代入可得![]() ,
,
解得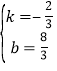 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(2)由(1)可知![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把点![]() 坐标代入可求得
坐标代入可求得![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
![]() 点到
点到![]() 轴的距离为
轴的距离为![]() ,
,
又由(1)可得![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 以点
以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,
为顶点的四边形是矩形,
![]() 为直角三角形,
为直角三角形,
①当![]() 时,则
时,则![]() 只能在
只能在![]() 轴上,连接
轴上,连接![]() 交
交![]() 于点
于点![]() ,如图1,
,如图1,
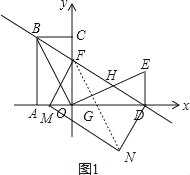
该情况不符合题意.
②当![]() 时,则
时,则![]() 只能在
只能在![]() 轴上,连接
轴上,连接![]() 交
交![]() 于点
于点![]() ,如图2,
,如图2,

则有![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,![]() ,
,
解得![]() ,
,![]() ,此时
,此时![]() ;
;
③当![]() 时,则可知
时,则可知![]() 点为
点为![]() 点,如图,
点,如图,
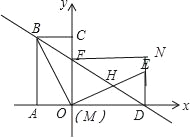
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
可求得![]() ;
;
综上可知存在满足条件的![]() 点,其坐标为
点,其坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
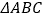 的三个顶点都在格点上,点
的三个顶点都在格点上,点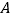 的坐标为
的坐标为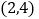 .
.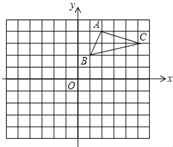
(1)画出
 关于
关于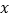 轴对称的
轴对称的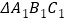 ,并写出点
,并写出点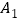 的坐标
的坐标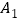 .
.(2)画出
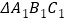 绕原点
绕原点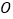 旋转后
旋转后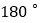 得到的
得到的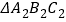 ,并写出
,并写出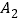 点的坐标
点的坐标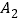 .
.(3)
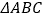 是否为直角三角形?答 (填是或者不是).
是否为直角三角形?答 (填是或者不是).(4)利用格点图,画出
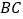 边上的高
边上的高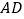 ,并求出
,并求出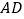 的长,
的长,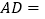 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2﹣ab﹣bc﹣ac=
 [(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
[(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.(1)请你检验说明这个等式的正确性.
(2)若a=2019,b=2020,c=2021,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗?
(3)若a﹣b=
 ,b﹣c=
,b﹣c= ,且a2+b2+c2=1,求ab+bc+ac的值.
,且a2+b2+c2=1,求ab+bc+ac的值. -
科目: 来源: 题型:
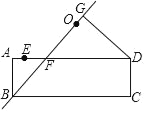
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为( )
A.
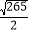 B.
B. 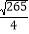 C.
C. 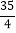 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们通常用作差法比较代数式大小.例如:已知M=2x+3,N=2x+1,比较M和N的大小.先求M﹣N,若M﹣N>0,则M>N;若M﹣N<0,则M<N;若M﹣N=0,则M=N,反之亦成立.本题中因为MN=2x+3(2x+1)=2>0,所以M>N.
(1)如图1是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S2.用含a的代数式表示S1= ,S2= (需要化简).然后请用作差法比较S1与S2大小;
(2)已知A=2a2﹣6a+1,B=a2﹣4a﹣1,请你用作差法比较A与B大小.
(3)若M=(a﹣4)2,N=16﹣(a﹣6)2,且M=N,求(a﹣4)(a﹣6)的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的扇形是一个圆锥的侧面展开图,若∠AOB=120°,弧AB的长为12πcm,则该圆锥的侧面积为 cm2 .

相关试题

