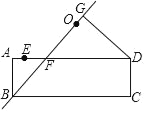
【题目】如图，矩形ABCD中，AB＝3，AD＝9，点E在边AD上，AE＝1，过E、D两点的圆的圆心O在边AD的上方，直线BO交AD于点F，作DG⊥BO，垂足为G．当△ABF与△DFG全等时，⊙O的半径为（　　）

A. B. C. D.

【答案】B

【解析】

根据全等三角形的性质得到BF=DF，根据矩形的性质得到∠A=90°，根据勾股定理得到AF=4，连接OE，OD，则OE=OD，过O作OH⊥AD于H，则HE=HD=4，根据相似三角形的性质得到OH=，根据勾股定理列方程即可得到结论．

解：∵△ABF与△DFG全等，
∴BF=DF，
∵AD=9，
∴BF=9-AF，
∵四边形ABCD是矩形，
∴∠A=90°，
∴AB2+AF2=BF2，
即32+AF2=（9-AF）2，
解得：AF=4，
∵AE=1，
∴EF=3，DE=8，
连接OE，OD，
则OE=OD，
过O作OH⊥AD于H，
则HE=HD=4，
∴FH=1，
∵∠A=∠OHF=90°，∠AFB=∠OFH，
∴△ABF∽△HOF，
∴＝，
即＝，
∴OH=，
在Rt△ODH中，OD==，


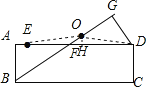
故选：B．

关闭