【题目】如图,在平面直角坐标系中,![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标为
的坐标为![]() .
.
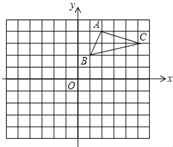
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标
的坐标![]() .
.
(2)画出![]() 绕原点
绕原点![]() 旋转后
旋转后![]() 得到的
得到的![]() ,并写出
,并写出![]() 点的坐标
点的坐标![]() .
.
(3)![]() 是否为直角三角形?答 (填是或者不是).
是否为直角三角形?答 (填是或者不是).
(4)利用格点图,画出![]() 边上的高
边上的高![]() ,并求出
,并求出![]() 的长,
的长,![]() .
.
参考答案:
【答案】(1)图形见解析,点![]() 的坐标
的坐标![]() ;(2)图形见解析,
;(2)图形见解析,![]() ;(3)不是,理由见解析;(4)
;(3)不是,理由见解析;(4)![]() .
.
【解析】
(1)依据![]() 与
与![]() 关于
关于![]() 轴对称,即可得到
轴对称,即可得到![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)依据![]() 绕原点
绕原点![]() 旋转
旋转![]() 后得到的
后得到的![]() 进行画图并写出点的坐标
进行画图并写出点的坐标![]() ;
;
(3)利用勾股定理的逆定理进行计算即可;
(4)利用格点图,画出![]() 边上的高
边上的高![]() ,依据
,依据![]() ,即可得到
,即可得到![]() 的长.
的长.
解:(1)如图所示,![]() 即为所求,点
即为所求,点![]() 的坐标
的坐标![]() ;
;
(2)如图所示,![]() ,点
,点![]() 的坐标
的坐标![]() ;
;
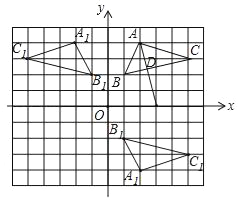
(3)![]() ,
,
![]() 不是直角三角形;
不是直角三角形;
(4)如图所示,![]() 边上的高
边上的高![]() 即为所求,
即为所求,
![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
故答案为:![]() ;
;![]() ;不是;
;不是;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点
 点
点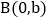 且a、b满足
且a、b满足 .
.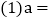 ______;
______;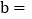 ______.
______.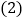 点P在直线AB的右侧,且
点P在直线AB的右侧,且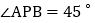 ,
, 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______; 若
若 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;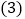 如图2,在
如图2,在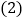 的条件下,
的条件下,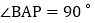 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接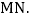 求证:
求证: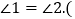 提示:过点P作
提示:过点P作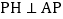 交x轴于
交x轴于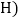
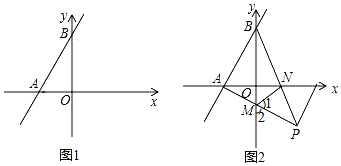
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
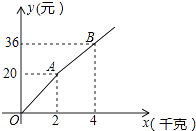
A.6
B.8
C.9
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2﹣ab﹣bc﹣ac=
 [(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
[(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.(1)请你检验说明这个等式的正确性.
(2)若a=2019,b=2020,c=2021,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗?
(3)若a﹣b=
 ,b﹣c=
,b﹣c= ,且a2+b2+c2=1,求ab+bc+ac的值.
,且a2+b2+c2=1,求ab+bc+ac的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是矩形,点
是矩形,点 、
、 在坐标轴上,
在坐标轴上,  是
是 绕点
绕点 顺时针旋转
顺时针旋转 得到的,点
得到的,点 在
在 轴上,直线
轴上,直线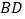 交
交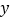 轴于点
轴于点 ,交
,交 于点
于点 ,线段
,线段 ,
, .
.
(1)求直线
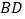 的解析式;
的解析式;(2)求
 的面积;
的面积;(3)点
 在
在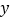 轴上,平面内是否存在点
轴上,平面内是否存在点 ,使以点
,使以点 、
、 、
、 、
、 为顶点的四边形是矩形?若存在,请直接写出点
为顶点的四边形是矩形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

