【题目】已知在平面直角坐标系中,过点![]() 向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作
向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作![]() 交y轴于点E,设点F运动的时间是t秒
交y轴于点E,设点F运动的时间是t秒![]() .
.
![]() 若点E在y轴的负半轴上
若点E在y轴的负半轴上![]() 如图所示
如图所示![]() ,求证:
,求证:![]() ;
;
![]() 如果点F运动时间是4秒.
如果点F运动时间是4秒.
![]() 求直线AE的表达式;
求直线AE的表达式;
![]() 若直线AE与x轴的交点为B,C是y轴上一点,使
若直线AE与x轴的交点为B,C是y轴上一点,使![]() ,求出C的坐标;
,求出C的坐标;
![]() 在点F运动过程中,设
在点F运动过程中,设![]() ,
,![]() ,试用含m的代数式表示n.
,试用含m的代数式表示n.
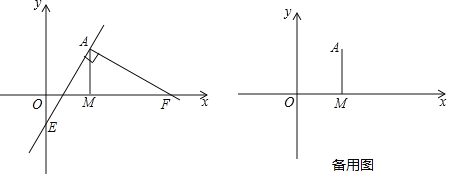
参考答案:
【答案】(1)见解析;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
![]() 点F的坐标为
点F的坐标为![]() ,求出点E的坐标为
,求出点E的坐标为![]() ,即可求解;
,即可求解;
![]() 把
把![]() 代入
代入![]() 式,即可求解,
式,即可求解,![]() 求出直线CH的表达式即可求解;
求出直线CH的表达式即可求解;
![]() ,
,![]() ,即可求解.
,即可求解.
![]() 点F的坐标为
点F的坐标为![]() ,直线AE交x轴于点B,
,直线AE交x轴于点B,
将点A、F坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得: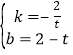 ,
,
![]() ,
,
![]() 直线AE表达式中的k值为
直线AE表达式中的k值为![]() ,
,
则直线AE的表达式为:![]() ,
,
则点B的坐标为![]() ,点E的坐标为
,点E的坐标为![]() ,
,
![]() ,
,
同理可得:![]() ;
;
![]() 把
把![]() 代入
代入![]() 式并解得:
式并解得:
直线AE的表达式为:![]() ,
,
![]() 如图取AB的中点H,过点H作直线AE的垂线交y轴于点C,
如图取AB的中点H,过点H作直线AE的垂线交y轴于点C,
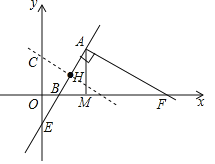
则直线CH表达式中的k值为:![]() ,
,
点B的坐标为![]() ,中点H的坐标为
,中点H的坐标为![]() ,
,
则设:直线CH的表达式为:![]() ,
,
将点H坐标代入上式并解得:![]() ,
,
即点C的坐标为![]() ;
;
![]() ,
,![]() ,
,
则:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
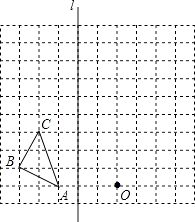
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 . -
科目: 来源: 题型:
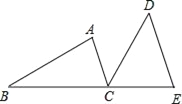
查看答案和解析>>【题目】如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用
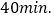 小亮骑自行车以
小亮骑自行车以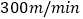 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程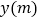 与各自离开出发地的时间
与各自离开出发地的时间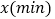 之间的函数图象如图所示,
之间的函数图象如图所示,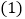 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______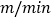 ;
;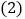 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;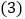 求两人相遇的时间.
求两人相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…

(1)观察图形并完成表格:图形名称
基本图形的个数
菱形的个数
图①
1
1
图②
2
3
图③
3
7
图④
4
…
…
…
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
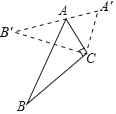
A. 65°B. 60°C. 50°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
相关试题

