【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
参考答案:
【答案】(1)乙机器每小时生产16个,丙机器每小时生产20个;(2)乙;31.5(3)使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环共需31小时.
【解析】
(1)设乙机器每小时生产4x个,则丙机器每小时生产5x个,依据甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.列一元一次方程即可解答;
(2)每次循环交替生产48个零件,那么最后一次循环是500除以48的余数,然后按顺序计算即可;
(3)速度快的先做即可.
(1)设乙机器每小时生产4x个,则丙机器每小时生产5x个,10小时25分钟=![]() 小时.依题意得:
小时.依题意得:
![]() (12+4x+5x)=500
(12+4x+5x)=500
解得:x=4,
乙机器每小时生产4x=16个,
丙机器每小时生产5x=20个,
答:乙机器每小时生产16个,丙机器每小时生产20个,
(2)500÷(12+16+20)=10……20,
按甲、乙、丙次序交替生产循环10次,共10×3=30小时,最后20个先由甲生产1小时12个,余下8个由乙生产8÷16=0.5小时,
∴整个生产过程共需30+1+0.5=31.5小时,
故答案为:乙;31.5
(3)使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环,生产循环10次,共10×3=30小时,最后20个由丙生产1小时即可,共需30+1=31小时.
答:使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环共需31小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,过点
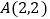 向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作
向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作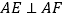 交y轴于点E,设点F运动的时间是t秒
交y轴于点E,设点F运动的时间是t秒 .
.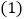 若点E在y轴的负半轴上
若点E在y轴的负半轴上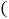 如图所示
如图所示 ,求证:
,求证: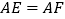 ;
;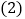 如果点F运动时间是4秒.
如果点F运动时间是4秒. 求直线AE的表达式;
求直线AE的表达式; 若直线AE与x轴的交点为B,C是y轴上一点,使
若直线AE与x轴的交点为B,C是y轴上一点,使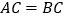 ,求出C的坐标;
,求出C的坐标; 在点F运动过程中,设
在点F运动过程中,设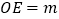 ,
,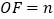 ,试用含m的代数式表示n.
,试用含m的代数式表示n.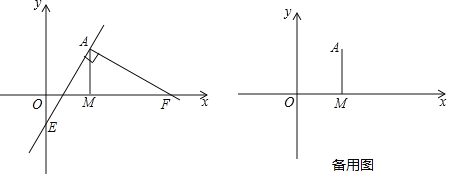
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…

(1)观察图形并完成表格:图形名称
基本图形的个数
菱形的个数
图①
1
1
图②
2
3
图③
3
7
图④
4
…
…
…
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
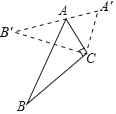
A. 65°B. 60°C. 50°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为
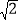 ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )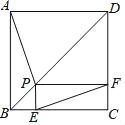
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线
 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.

请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
相关试题

