Question

【题目】如图，∠AOB的一边OA为平面镜，∠AOB=38°，在OB上有一点E ， 从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是（ ）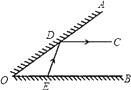

A.76°
B.52°
C.45°
D.38°

Answer 1

【答案】A
【解析】由镜面反射的原理可知∠ODE=∠ADC ，
∵ CD//OB，
∴∠ADC=∠AOB=38°，
∴∠ODE=∠ADC=38°，
∴∠BED=∠ODE+∠ODE=38°+38°=76°，
故选A.
由镜面反射的原理可知∠ODE=∠ADC ， 由CD//OB可得∠ADC=∠AOB ， 从而求出∠ODE ， 所以可根据三角形的外角性质求出∠BED；或根据平角的定义求出∠CDE ， 再根据平行线的性质可得∠CDE+∠BED=180°，可求出∠BED.