【题目】洋芋是大多数云南人都喜爱的食品,现有20袋洋芋,以每袋450斤为标准,超过或不足的斤数分别用正、负数来表示,与标准质量的差值记录如表:
每袋与标准质量的差值(斤) | ﹣5 | ﹣2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这20袋洋芋中,最重的一袋比最轻的一袋重几斤?
(2)这20袋洋芋的平均质量比标准质量多还是少?多或少几斤?
(3)求这20袋洋芋的总质量.
参考答案:
【答案】(1)11斤;(2)多1.2斤;(3)9024斤.
【解析】
(1)找出最重的与最轻的,即可求出差值;
(2)求出平均质量,比较标准即可;
(3)求出总重量即可.
(1)根据题意得:最重的一袋为456斤,最轻的一袋为445斤,
则这20袋洋芋中,最重的一袋比最轻的一袋重11斤;
(2)根据题意得:52×4+0×3+1×4+3×5+6×3=24,
24![]() 20=1.2(斤)
20=1.2(斤)
这20袋洋芋的平均质量比标准质量多,多1.2斤.
(3)根据题意得:450×20+24=9024(斤),
则这20袋洋芋的总质量9024斤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
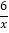 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-
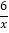 <0时x的取值范围;
<0时x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=mx+5的图象与反比例函数y=
 (k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.(1)求一次函数和反比例函数的解析式;
(2)求△OAM的面积S;
(3)在y轴上求一点P,使PA+PB最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
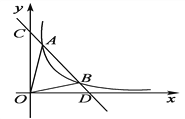
查看答案和解析>>【题目】如图,已知A(-4,
 ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y= (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(1)、根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)、求一次函数解析式及m的值;
(3)、P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A,B,与双曲线y=
 在第一象限内交于点C(1,m).
在第一象限内交于点C(1,m).(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线y=
 交于点P,Q,求△APQ的面积.
交于点P,Q,求△APQ的面积.
-
科目: 来源: 题型:
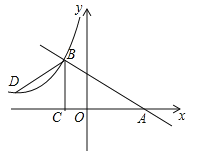
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数
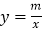 (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
相关试题

