【题目】在Rt△ABC中,AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,求半径r的取值范围
参考答案:
【答案】解:过点C作CD⊥AB于点D,
∵AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,
∴AB=5,
当直线与圆相切时,d=r,圆与斜边AB只有一个公共点,圆与斜边AB只有一个公共点,
∴CD×AB=AC×BC,∴CD=r= ![]()
当直线与圆如图所示也可以有一个交点,
∴3<r≤4,
故答案为:3<r≤4或r= ![]()

【解析】根据直线与圆的位置关系得出相切时有一交点,再结合图形得出另一种有一个交点的情况,即可得出答案.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如上图,反比例函数
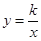 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .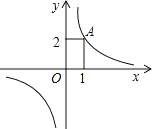
【答案】(-1,-2)(答案不唯一).
【解析】试题分析:根据“第一象限内的图象经过点A(1,2)”先求出函数解析式,给x一个值负数,求出y值即可得到坐标.
试题解析:∵图象经过点A(1,2),
∴
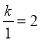
解得k=2,
∴函数解析式为y=
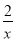 ,
,当x=-1时,y=
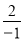 =-2,
=-2,∴P点坐标为(-1,-2)(答案不唯一).
考点:反比例函数图象上点的坐标特征.
【题型】填空题
【结束】
13【题目】在y轴右侧且平行于y轴的直线l被反比例函数
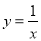 (
(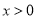 )与函数
)与函数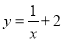 (
(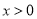 )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位. 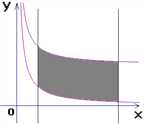
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、
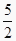 为半径的圆的位置关系是( )
为半径的圆的位置关系是( )
A.相切
B.相交
C.相离
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值
(单位:g) 5
5 2
20
1
3
6
袋 数
1
4
3
4
5
3
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发多少秒直线CD恰好与⊙B相切.
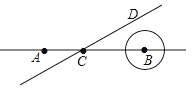
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,求l沿OC所在直线向下平移多少cm时与⊙O相切.

相关试题

