【题目】如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.
参考答案:
【答案】解:如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OB∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′= ![]() =
= ![]()
∴当过点P且与OB平行的直线与⊙O有公共点时,0<OP≤ ![]()
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0<OP≤ ![]()
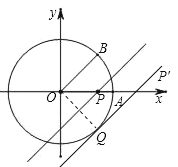
【解析】将过点P且与OB平行的直线平移至P′的位置,使其与⊙O相切,设切点为Q,连接OQ,根据条件证明△OQP′为等腰直角三角形,已知OQ=1,解直角三角形求OP′,确定OP的取值范围
【考点精析】通过灵活运用直线与圆的三种位置关系和切线的性质定理,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、
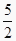 为半径的圆的位置关系是( )
为半径的圆的位置关系是( )
A.相切
B.相交
C.相离
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值
(单位:g) 5
5 2
20
1
3
6
袋 数
1
4
3
4
5
3
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,求半径r的取值范围
-
科目: 来源: 题型:
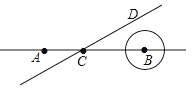
查看答案和解析>>【题目】如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发多少秒直线CD恰好与⊙B相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,求l沿OC所在直线向下平移多少cm时与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在y轴右侧且平行于y轴的直线l被反比例函数
 (
( )与函数
)与函数 (
( )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位. 
【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=
 (x>0)与函数y=
(x>0)与函数y= +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
【题型】填空题
【结束】
14【题目】函数
 的图象如右图所示,则结论:
的图象如右图所示,则结论:①两函数图象的交点
 的坐标为
的坐标为 ; ②当
; ②当 时,
时,  ;
;③当
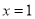 时,
时,  ; ④当
; ④当 逐渐增大时,
逐渐增大时,  随着
随着 的增大而增大,
的增大而增大,  随着
随着 的增大而减小.
的增大而减小.其中正确结论的序号是 .

相关试题

