【题目】如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,求l沿OC所在直线向下平移多少cm时与⊙O相切.
参考答案:
【答案】解:∵直线和圆相切时,OH=5,
又∵在直角三角形OHA中,HA= ![]() =4,OA=5,
=4,OA=5,
∴OH=3.
∴需要平移5-3=2cm.故答案为:2.
【解析】根据直线和圆相切,则只需满足OH=5.又由垂径定理构造直角三角形可求出此时OH的长,从而计算出平移的距离.
【考点精析】关于本题考查的垂径定理和直线与圆的三种位置关系,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,求半径r的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.

-
科目: 来源: 题型:
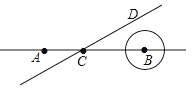
查看答案和解析>>【题目】如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发多少秒直线CD恰好与⊙B相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在y轴右侧且平行于y轴的直线l被反比例函数
 (
( )与函数
)与函数 (
( )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位. 
【答案】8
【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=
 (x>0)与函数y=
(x>0)与函数y= +2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
+2(x>0)所截,∴设它们的交点为A,C,∴AC=2,∵直线l向右平移4个单位,∴CD=4,∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位.故答案为8.
【题型】填空题
【结束】
14【题目】函数
 的图象如右图所示,则结论:
的图象如右图所示,则结论:①两函数图象的交点
 的坐标为
的坐标为 ; ②当
; ②当 时,
时,  ;
;③当
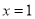 时,
时,  ; ④当
; ④当 逐渐增大时,
逐渐增大时,  随着
随着 的增大而增大,
的增大而增大,  随着
随着 的增大而减小.
的增大而减小.其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
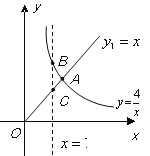
查看答案和解析>>【题目】函数
 的图象如右图所示,则结论:
的图象如右图所示,则结论:①两函数图象的交点
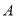 的坐标为
的坐标为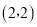 ; ②当
; ②当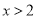 时,
时,  ;
;③当
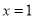 时,
时, 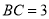 ; ④当
; ④当 逐渐增大时,
逐渐增大时, 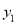 随着
随着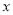 的增大而增大,
的增大而增大, 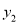 随着
随着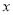 的增大而减小.
的增大而减小.其中正确结论的序号是 .
【答案】①③④
【解析】试题分析:反比例函数与一次函数的交点问题.运用一次函数和反比例函数的性质来解决的一道常见的数形结合的函数试题.一次函数和反比例函数的交点坐标就是一次函数与反比例函数组成的方程组的解.根据k>0确定一次函数和反比例函数在第一象限的图象特征来确定其增减性;根据x=1时求出点B点C的坐标从而求出BC的值;当x=2时两个函数的函数值相等时根据图象求得x>2时y1>y2.
试题解析:①由一次函数与反比例函数的解析式
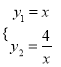 ,
,解得,
 ,
,∴A(2,2),故①正确;
②由图象得x>2时,y1>y2;故②错误;
③当x=1时,B(1,3),C(1,1),∴BC=3,故③正确;
④一次函数是增函数,y随x的增大而增大,反比例函数k>0,y随x的增大而减小.故④正确.
∴①③④正确.
考点:反比例函数与一次函数的交点问题.
【题型】填空题
【结束】
15【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点
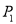 、
、 在函数
在函数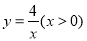 的图象上,斜边
的图象上,斜边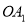 、
、 都在
都在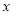 轴上,则点
轴上,则点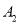 的坐标是____________.
的坐标是____________.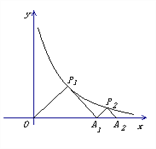
相关试题

