【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD 
(1)求证:AD是⊙O的切线;
(2)若tan∠F= ![]() ,⊙O半径为1,求线段AD的长.
,⊙O半径为1,求线段AD的长.
参考答案:
【答案】
(1)解:连接OC.
∵OE⊥AC,
∴AE=CE,
∴DC=DA,
在△OCD与△OAD中,  ,
,
∴△OCD≌△OAD,
∵FD切⊙O于D,
∴∠OCD=∠OAD=90°,
∴AD是⊙O的切线
(2)解:设AD=x,
∵tan∠F= ![]() ,OC=1,
,OC=1,
∴在Rt△OCF中, ![]() =
= ![]() ,
,
∴FC=2,
在Rt△ADF中,同理可得,FO=2x﹣1,
∴在Rt△OCF中,
FO2=FC2+CO2,
∴(2x﹣1)2=5,解得x1= ![]() ,x2=
,x2= ![]() (舍去),
(舍去),
即 AD= ![]() .
.

【解析】(1)连接OC.根据垂径定理得到AE=CE,根据全等三角形和切线的性质得到∠OCD=∠OAD=90°,于是得到结论;(2)设AD=x,根据三角函数的定义得到FC=2,在Rt△ADF中,同理可得,FO=2x﹣1,根据勾股定理即可得到结论.
【考点精析】利用垂径定理和解直角三角形对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线与点F,连接BF.

(1)求证:四边形ADBF是平行四边形;
(2)若∠ADF=∠BDF,DF=2CD,求∠ABC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.

(1)求B处到小岛C的距离
(2)若轮船从B处继续向东方向航行,有无触礁危险?请说明理由.
(参考数据: ≈1.73)
≈1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形的边长为4,甲、乙两动点分别从正方形
 的顶点
的顶点 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )
同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )
A.
 边上 B.
边上 B.  边上 C.
边上 C.  边上 D.
边上 D.  边上
边上 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) 5(x+8)=6(2x-7)+5; (2) 5-
 =x;
=x;(3)
 -
- =1; (4)
=1; (4)  -
- =1;
=1; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y1=
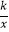 的图象与一次函数y2=
的图象与一次函数y2=  x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= 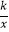 的图象上.
的图象上. 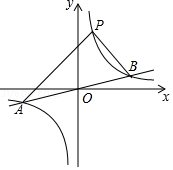
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

相关试题

