Question

【题目】如图，反比例函数y1= 的图象与一次函数y2= x的图象交于点A、B，点B的横坐标是4，点P（1，m）在反比例函数y1= 的图象上．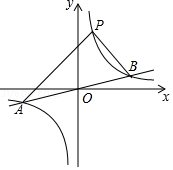
（1）求反比例函数的表达式；
（2）观察图象回答：当x为何范围时，y1＞y2；
（3）求△PAB的面积．

Answer 1

【答案】
（1）解：把x=4代入y2= x，得到点B的坐标为（4，1），

把点B（4，1）代入y1= ，得k=4．

反比例函数的表达式为y1=

（2）解：∵点A与点B关于原点对称，

∴A的坐标为（﹣4，﹣1），

观察图象得，当x＜﹣4或0＜x＜4时，y1＞y2

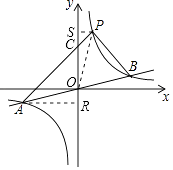
（3）解：过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，

设AP与y轴交于点C，如图，

∵点A与点B关于原点对称，

∴OA=OB，

∴S△AOP=S△BOP，

∴S△PAB=2S△AOP．

y1= 中，当x=1时，y=4，

∴P（1，4）．

设直线AP的函数关系式为y=mx+n，

把点A（﹣4，﹣1）、P（1，4）代入y=mx+n，

则 ，

解得 ．

故直线AP的函数关系式为y=x+3，

则点C的坐标（0，3），OC=3，

∴S△AOP=S△AOC+S△POC

= OCAR+ OCPS

= ×3×4+ ×3×1

= ，

∴S△PAB=2S△AOP=15．

【解析】（1）把x=4代入y2= x，得到点B的坐标，再把点B的坐标代入y1= ，求出k的值，即可得到反比例函数的表达式；（2）观察图象可知，反比例函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式y1＞y2的解集；（3）过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，设AP与y轴交于点C，由点A与点B关于原点对称，得出OA=OB，那么S△AOP=S△BOP ， S△PAB=2S△AOP ． 求出P点坐标，利用待定系数法求出直线AP的函数关系式，得到点C的坐标，根据S△AOP=S△AOC+S△POC求出S△AOP= ，则S△PAB=2S△AOP=15．