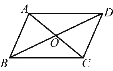
【题目】如图,ABCD的对角线AC,BD相交于点O,△ABO的周长为23 cm,AD比CD长2 cm,AC+BD=34 cm.求ABCD的周长.
参考答案:
【答案】28
【解析】
设CD=AB=xcm,则AD=(2+x)cm,再由AC与BD的和为34cm求出OA+OB的长,根据△ABO的周长为23cm求出x的值,进而可得出结论.
解:∵四边修改ABCD是平行四边形,
∴设CD=AB=xcm,则AD=(2+x)cm.
∵AC与BD的和为34cm,
∴OA+OB=17cm.
∵△ABO的周长为23cm,
∴AB=23-17=6(cm),
∴AD=6+2=8cm,
∴ABCD的周长=2(AB+AD)=2(6+8)=28(cm).
答:ABCD的周长是28cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘,
 为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
(1)某顾客在该商场消费40元,是否可以获得转动转盘的机会?
(2)某顾客在该商场正好消费66元,则他转动一次转盘,获得三种打折优惠的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和四边形CDHN都是正方形.AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,求证:FM=MH,FM⊥MH;
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,求证:△FMH是等腰直角三角形;
(3)将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图是理论上接近完美的作图方式,乐乐很喜欢用尺规画出要求的图形.在下面的
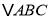 中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.
中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.(1)作出
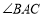 的平分线交
的平分线交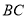 边于点
边于点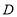 ;
;(2)作出
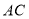 边上的垂直平分线
边上的垂直平分线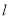 交
交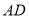 于点
于点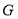 ;
;(3)连接
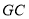 ,若
,若 ,则
,则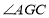 的度数为 .
的度数为 .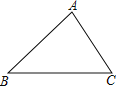
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的操作过程,回答后面的问题:在一次数学实践探究活动中,小强过A,C两点画直线AC把平行四边形ABCD分割成两个部分(如图1),小刚过AB,CD的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图2).

(1)这两种分割方法中面积之间的关系为:S1 S2,S3 S4;
(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上面积关系的直线有 条,请在图3的平行四边形中画出一种;
(3)由上述实验操作过程,你发现了什么规律?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

相关试题

