【题目】在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和四边形CDHN都是正方形.AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,求证:FM=MH,FM⊥MH;
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,求证:△FMH是等腰直角三角形;
(3)将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必说明理由)

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△FMH还是等腰直角三角形.
【解析】
(1)根据正方形的性质可得FB=BM=MD=DH,然后利用“边角边”证明△FBM和△MDH全等,根据全等三角形对应边相等可得FM=MH,再求出∠FMH=90°,得到FM⊥HM,然后根据等腰直角三角形的定义证明即可;(2)连接MB、MD,设FM与AC交于点P,根据三角形的中位线平行于第三边并且等于第三边的一半可得MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,然后得到四边形BCDM是平行四边形并求出∠CBM=∠CDM,再求出∠FBM=∠MDH,然后利用“边角边”证明△FBM和△MDH全等,根据全等三角形对应边相等可得FM=MH,全等三角形对应角相等可得∠MFB=∠HMD,根据两直线平行,内错角相等可得∠APM=∠FMD,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠FMH=∠FBP=90°,再根据等腰直角三角形的定义证明即可;(3)证明方法同(2).
(1)证明:∵四边形BCGF为正方形,
∴BF=BM=MN,∠FBM=90°,
∵四边形CDHN为正方形,
∴DM=DH=MN,∠HDM=90°,
∵BF=BM=MN,DM=DH=MN,
∴BF=BM=DM=DH,
∵BF=DH,∠FBM=∠HDM,BM=DM,
∴△FBM≌△HDM,
∴FM=MH,
∵∠FMB=∠DMH= 45°,
∴∠FMH=90°,
∴FM⊥HM.
(2)证明:连接MB、MD,如图2,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=![]() AC=BC=BF;MB∥CD,且MB=
AC=BC=BF;MB∥CD,且MB=![]() CE=CD=DH,
CE=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
∵∠FBP=∠HDC,
∴∠FBM=∠MDH,
∵MD =BF,∠FBM=∠MDH,MB=DH,
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠APM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠APM-∠MFB=∠FBP=90°,
∴△FMH是等腰直角三角形;

(3)△FMH还是等腰直角三角形.
连接MB、MD,如图3,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD=BC=BF;MB∥CD,且MB=CD=DH,
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
又∵∠FBP=∠HDC,
∴∠FBM=∠MDH,
在△FBM和△MDH中,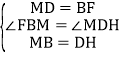 ,
,
∴△FBM≌△MDH(SAS),
∴FM=MH,且∠MFB=∠HMD,
∵BC∥MD,
∴∠APM=∠FMD,
∴∠FMH=∠FMD-∠HMD=∠APM-∠MFB=∠FBP=90°,
∴△FMH是等腰直角三角形.
-
科目: 来源: 题型:
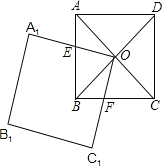
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC和BD相交于点O,O又是正方形A1B1C1O的一个顶点,OA1交AB于点E,OC1交BC于点F.
(1)求证:△AOE≌△BOF;
(2)如果两个正方形的边长都为a,那么正方形A1B1C1O绕O点转动,两个正方形重叠部分的面积等于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形底角的度数为( )
A.50°B.65°C.65°或25°D.50°或40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘,
 为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
(1)某顾客在该商场消费40元,是否可以获得转动转盘的机会?
(2)某顾客在该商场正好消费66元,则他转动一次转盘,获得三种打折优惠的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图是理论上接近完美的作图方式,乐乐很喜欢用尺规画出要求的图形.在下面的
 中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.
中,请你也按要求用尺规作出下列图形(不写作法,但要保留作图痕迹)并填空.(1)作出
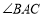 的平分线交
的平分线交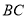 边于点
边于点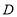 ;
;(2)作出
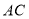 边上的垂直平分线
边上的垂直平分线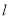 交
交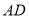 于点
于点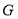 ;
;(3)连接
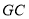 ,若
,若 ,则
,则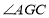 的度数为 .
的度数为 .
-
科目: 来源: 题型:
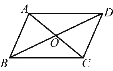
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△ABO的周长为23 cm,AD比CD长2 cm,AC+BD=34 cm.求ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的操作过程,回答后面的问题:在一次数学实践探究活动中,小强过A,C两点画直线AC把平行四边形ABCD分割成两个部分(如图1),小刚过AB,CD的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图2).

(1)这两种分割方法中面积之间的关系为:S1 S2,S3 S4;
(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上面积关系的直线有 条,请在图3的平行四边形中画出一种;
(3)由上述实验操作过程,你发现了什么规律?
相关试题

