【题目】已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
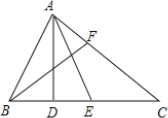
参考答案:
【答案】证明见解析.
【解析】
试题连接EF.根据角平分线的性质知AF:FC=DE:EC,由平行线分线段成比例知AF:FC=DE:EC,由这两个比例式和已知条件“BE=CE”知![]() ,即AB=2DE.
,即AB=2DE.
试题解析: 连接EF.
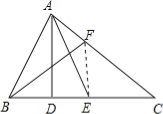
∵∠ABC=2∠C,BF为∠B的平分线,
∴∠FBC=∠C=![]() ∠ABC,
∠ABC,
∴BF=CF;
又∵BE=CE,
∴EF⊥BC;
∵AD⊥BC,
∴EF∥AD,
∴AF:FC=DE:EC;
而AB:BC=AF:FC,
∴AB:BC=DE:EC,
∴![]() ,
,
即AB=2DE.
考点: 1.平行线分线段成比例;2.角平分线的性质;3.等腰三角形的判定与性质.
-
科目: 来源: 题型:
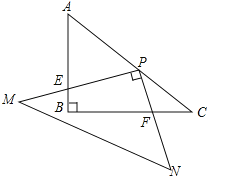
查看答案和解析>>【题目】如图,在
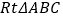 中,
中, ,
,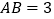 ,
, ,
,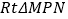 ,
,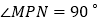 ,点
,点 在
在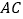 上,
上,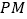 交
交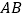 于点
于点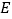 ,
,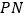 交
交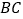 于点
于点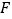 ,当
,当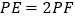 时,
时,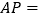 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请按步骤画出函数
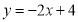 的图象,根据图象回答下列问题:
的图象,根据图象回答下列问题:(1)
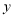 的值随
的值随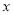 值的增大而 ;
值的增大而 ;(2)图象与
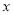 轴的交点坐标是 ,与
轴的交点坐标是 ,与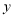 轴的交点坐标是 ;
轴的交点坐标是 ;(3)当
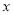 时,
时,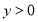 .
. -
科目: 来源: 题型:
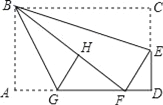
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=
 S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.其中正确的是__.(把所有正确结论的序号都选上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E是平行四边形ABCD中DA边的延长线上一点,且AE=AD,连接EC分别交AB,BE于点F、G.
(1)求证:BF=AF;
(2)若BD=12cm,求DG的长.

-
科目: 来源: 题型:
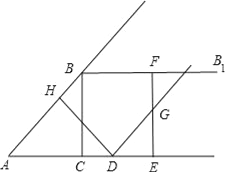
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,是摆放在张明和赵华面前的甲和乙两个圆柱形水槽从正面看到的图形,甲槽中有适量的水,乙槽中有一圆柱形铁块(圆柱形铁块的下底面完全落在水槽底面,铁块的高度低于水槽的高度).张明将甲槽中的水匀速注入乙槽,同时赵华计时并测量,最后他们把甲、乙两个水槽中水的深度
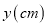 与注水时间
与注水时间 之间的关系画出了如图所示的函数图象.请根据函数图象提供的信息,解答下列问题:
之间的关系画出了如图所示的函数图象.请根据函数图象提供的信息,解答下列问题:(1)如图所示,线段
 表示 槽中水的深度与注水时间之间的关系;折线
表示 槽中水的深度与注水时间之间的关系;折线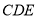 表示 槽中水的深度与注水时间之间的关系(以上两空填“甲” 或“乙”);点
表示 槽中水的深度与注水时间之间的关系(以上两空填“甲” 或“乙”);点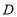 的纵坐标14表示的实际意义是 ;
的纵坐标14表示的实际意义是 ;(2)分别求线段
 、线段
、线段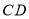 的函数表达式;
的函数表达式;(3)注水多长时间时,甲、乙两个水槽中水的深度相同?
(4)若乙水槽的底面积为
 (水槽壁的厚度不计),求乙水槽中铁块的体积是多少
(水槽壁的厚度不计),求乙水槽中铁块的体积是多少 ?
?

相关试题

