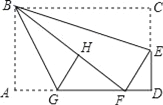
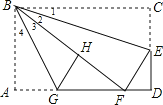
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
参考答案:
【答案】①③④
【解析】试题解析:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,
∴AF=![]() =8,
=8,
∴DF=AD-AF=10-8=2,
设EF=x,则CE=x,DE=CD-CE=6-x,
在Rt△DEF中,∵DE2+DF2=EF2,
∴(6-x)2+22=x2,解得x=![]() ,
,
∴ED= ![]() ,
,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;
HF=BF-BH=10-6=4,
设AG=y,则GH=y,GF=8-y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8-y)2,解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D,![]() ,
,![]() ,
,
∴![]() ,
,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG=![]() 63=9,S△FGH=
63=9,S△FGH=![]() GHHF=
GHHF=![]() ×3×4=6,
×3×4=6,
∴S△ABG=![]() S△FGH,所以③正确;
S△FGH,所以③正确;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
∴①③④正确.
-
科目: 来源: 题型:
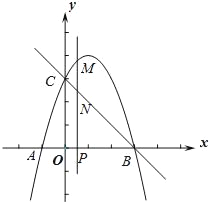
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
-
科目: 来源: 题型:
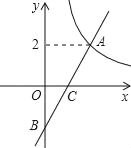
查看答案和解析>>【题目】已知,在平面直角坐标系xOy中,函数y=
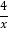 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了配合足球进校园的活动,实验学校在体育用品专卖店购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。求购买一个甲种足球,一个乙种足球各需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,-1)、B(2,0)、C(0,3),AC交
 轴于点D,AB交
轴于点D,AB交 轴于点E.
轴于点E.(1)△ABC的面积为________;
(2)点E的坐标为________;
(3)若点P的坐标为(0,
 ):
):①线段EP的长为________(用含
 的式子表示);
的式子表示);②当
 时,求点P的坐标。
时,求点P的坐标。
相关试题

