【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”给出下列定义: 若
的“非常距离”给出下列定义: 若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() . 例如:点
. 例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与
与![]() 的“非常距离”为
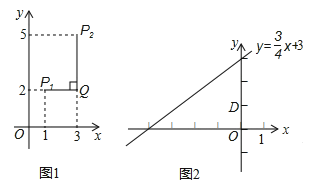
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点Q为垂直于
长度的较大值(点Q为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点A![]() ,B为
,B为![]() 轴上一个动点.
轴上一个动点.
①若点B(0,3),则点A与点B的“非常距离”为 ;
②若点A与点B的“非常距离”为2,则点B的坐标为 ;
③直接写出点A与点B的“非常距离”的最小值 .
(2)已知点D(0,1)点C是直线![]() 上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
参考答案:
【答案】(1)①3,②(0,2)或(0,-2) ③![]() (2)
(2)![]()
【解析】试题分析:(1)①根据若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|解答即可;
②根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0-y|=2,据此可以求得y的值;
③设点B的坐标为(0,y).因为|-![]() -0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-
-0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-![]() -0|=
-0|=![]() ;
;
(2)设点C的坐标为(x0, ![]() x0+3).根据材料“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”知,C、D两点的“非常距离”的最小值为-x0=
x0+3).根据材料“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”知,C、D两点的“非常距离”的最小值为-x0=![]() x0+2,据此可以求得点C的坐标.
x0+2,据此可以求得点C的坐标.
试题解析:(1)∵|-![]() -0|=
-0|=![]() ,|0-3|=3,
,|0-3|=3,
∴![]() <3,
<3,
∴点A与点B的“非常距离”为3.
②∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|-![]() -0|=
-0|=![]() ≠2,
≠2,
∴|0-y|=2,
解得,y=2或y=-2;
∴点B的坐标是(0,2)或(0,-2),
③点A与点B的“非常距离”的最小值为![]() .
.
(2)如图2,取点C与点D的“非常距离”的最小值时,

需要根据运算定义“若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|”解答,
此时|x1-x2|=|y1-y2|,即AC=AD,
∵C是直线y=![]() x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0, ![]() x0+3),
x0+3),
∴-x0=![]() x0+2,
x0+2,
此时,x0=-![]() ,
,
∴点C与点D的“非常距离”的最小值为:|x0|=![]() ,
,
此时C(-![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣1)2+1的顶点坐标是( )
A.(1,1)
B.(1,﹣1)
C.(﹣1,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
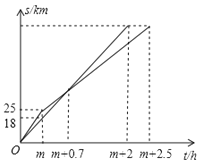
查看答案和解析>>【题目】在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以akm/h,bkm/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图所示,观察图象,下列说法:
①出发mh内小明的速度比小刚快;② a=26;③小刚追上小明时离起点43km;④此次越野赛的全程为90km,正确的有______________(把正确结论的序号填在横线上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙A的半径AB长是5,点C在AB上,且AC=3,如果⊙C与⊙A有公共点,那么⊙C的半径长r的取值范围是( )
A. r≥2 B. r≤8 C. 2<r<8 D. 2≤r≤8
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角是它的余角的3倍,则这个角的补角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(1,﹣3),B(2,﹣2),现将线段AB平移至A1B1,如果A1(a,1),B1(5,b),那么ab的值是( )
A.32B.16C.5D.4
相关试题

