【题目】一个角是它的余角的3倍,则这个角的补角是 .
参考答案:
【答案】112.5°
【解析】解:设这个角为x,则它的余角为(90°﹣x), 由题意得,x=3(90°﹣x),
解得:x=67.5°,
则这个角的补角=180°﹣67.5°=112.5°.
所以答案是:112.5°.
【考点精析】通过灵活运用余角和补角的特征,掌握互余、互补是指两个角的数量关系,与两个角的位置无关即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙A的半径AB长是5,点C在AB上,且AC=3,如果⊙C与⊙A有公共点,那么⊙C的半径长r的取值范围是( )
A. r≥2 B. r≤8 C. 2<r<8 D. 2≤r≤8
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:在平面直角坐标系
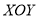 中,对于任意两点
中,对于任意两点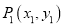 与
与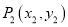 的“非常距离”给出下列定义: 若
的“非常距离”给出下列定义: 若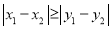 ,则点
,则点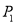 与
与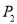 的“非常距离”为
的“非常距离”为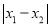 ;
;若
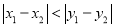 ,则点
,则点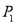 与
与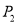 的“非常距离”为
的“非常距离”为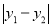 . 例如:点
. 例如:点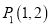 ,点
,点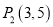 ,因为
,因为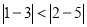 ,所以点
,所以点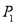 与
与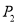 的“非常距离”为
的“非常距离”为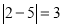 ,也就是图1中线段
,也就是图1中线段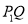 与线段
与线段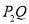 长度的较大值(点Q为垂直于
长度的较大值(点Q为垂直于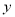 轴的直线
轴的直线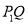 与垂直于
与垂直于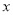 轴的直线
轴的直线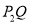 的交点).
的交点).(1)已知点A
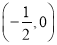 ,B为
,B为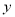 轴上一个动点.
轴上一个动点.①若点B(0,3),则点A与点B的“非常距离”为 ;
②若点A与点B的“非常距离”为2,则点B的坐标为 ;
③直接写出点A与点B的“非常距离”的最小值 .
(2)已知点D(0,1)点C是直线
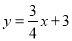 上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.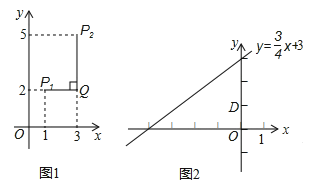
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(1,﹣3),B(2,﹣2),现将线段AB平移至A1B1,如果A1(a,1),B1(5,b),那么ab的值是( )
A.32B.16C.5D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种品的标价为120元,若以九折降价出售,仍获利20%,该商品的进货价为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华为手机营销按批量投入市场,第一次投放20000台,第三次投放80000台,每次按相同的增长率投放,设增长率为x,则可列方程( )
A.20000(1+x)2=80000
B.20000(1+x)+20000(1+x)2=80000
C.20000(1+x2)=80000
D.20000+20000(1+x)+20000(1+x)2=80000
相关试题

