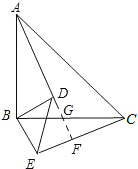
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由等腰直角三角形的性质得出AB=BC,BD=BE,∠ABC=∠DBE=90°,得出∠ABD=CBE,证出△ABD≌△CBE(SAS),得出AD=CE;
(2)△ABD≌△CBE得出∠BAD=∠BCE,再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,得出∠AFC=∠ABC=90°,证出结论.
(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=CBE,
在△ABD和△CBE中,
 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE;
(2)延长AD分别交BC和CE于G和F,如图所示:
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,2),其部分图象如图所示,给出下列四个结论: ①a<0; ②b2﹣4ac>0;③2a﹣b=0;④若点P(x0 , y0)在抛物线上,则ax02+bx0+c≤a﹣b+c.其中结论正确的是( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有500名学生.为了解全校每名学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到扇形统计图如右图:
(1)本次调查的个体是 ,样本容量是 ;
(2)扇形统计图中,乘私家车部分对应的圆心角是 度;
(3)请估计该校500名学生中,选择骑车和步行上学的一共有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=40°,∠DAE=15°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx﹣4k+5的图象与反比例函数y=
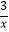 (x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 .
(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 . 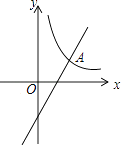
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,DE=1cm,求BD的长.

-
科目: 来源: 题型:
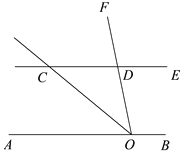
查看答案和解析>>【题目】如图,AB∥CD,点O是直线AB上一点,OC平分∠AOF.
(1)求证:∠DCO=∠COF;
(2)若∠DCO=40°,求∠EDF的度数.
相关试题

