【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 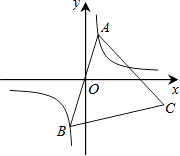
参考答案:
【答案】﹣6
【解析】解:∵双曲线y= ![]() 关于原点对称, ∴点A与点B关于原点对称.
关于原点对称, ∴点A与点B关于原点对称.
∴OA=OB.
连接OC,如图所示.
∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°.
∴tan∠OAC= ![]() =
= ![]() .
.
∴OC= ![]() OA.
OA.
过点A作AE⊥y轴,垂足为E,
过点C作CF⊥y轴,垂足为F,
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF.
∴△AEO∽△OFC.
∴ ![]() =
= ![]() =
= ![]() .
.
∵OC= ![]() OA,
OA,
∴OF= ![]() AE,FC=
AE,FC= ![]() EO.
EO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OF= ![]() AE=
AE= ![]() a,FC=
a,FC= ![]() EO=
EO= ![]() b.
b.
∵点A在双曲线y= ![]() 上,
上,
∴ab=2.
∴FCOF= ![]() b
b ![]() a=3ab=6
a=3ab=6
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FCOF=x(﹣y)=﹣xy
=6.
∴xy=﹣6.
∵点C在双曲线y= ![]() 上,
上,
∴k=xy=﹣6.
故答案为:﹣6.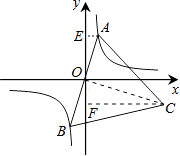
连接OC,易证AO⊥OC,OC= ![]() OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF=
OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF= ![]() AE,FC=
AE,FC= ![]() EO..设点A坐标为(a,b)则ab=2,可得FCOF=6.设点C坐标为(x,y),从而有FCOF=﹣xy=﹣6,即k=xy=﹣6.
EO..设点A坐标为(a,b)则ab=2,可得FCOF=6.设点C坐标为(x,y),从而有FCOF=﹣xy=﹣6,即k=xy=﹣6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③
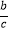 <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 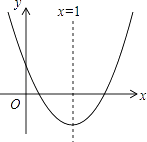
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2
 ,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
A.3
B.3+
C.2
D.2+
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多
 元,用
元,用 元购得的排球数量与用
元购得的排球数量与用 元购得的足球数量相等.
元购得的足球数量相等.⑴排球和足球的单价各是多少元?
⑵若恰好用去
 元,有哪几种购买方案?
元,有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
(﹣2)÷2=﹣1
(2)请用你发现的规律求出图④中的数x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2018的坐标是________.

相关试题

