【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③ ![]() <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 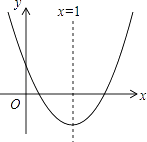
A.1
B.2
C.3
D.4
参考答案:
【答案】D
【解析】解:∵抛物线开口向上,与y轴的交点在x轴上方, ∴a>0,c>0,
∵对称轴为x=1,
∴﹣ ![]() =1,
=1,
∴b=﹣2a<0,
∴b<0,故①正确;
∴a+b=a﹣2a=﹣a<0,
∴a+b<0,故②正确;
∵顶点在第四象限,
∴ ![]() <0,
<0,
∴4ac﹣b2<0,
∴4×(﹣ ![]() )c﹣b2<0,
)c﹣b2<0,
∴﹣2bc﹣b2<0,
∴2bc+b2>0,
∴2c+b<0,
∴b<﹣2c,
∴ ![]() <﹣2,故③正确;
<﹣2,故③正确;
∵|n﹣1|=|2﹣n﹣1|,
∴an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),故④正确;
综上可知正确的结论有4个,
故选D.
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本,需要知道二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
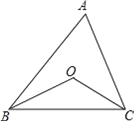
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2
 ,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
A.3
B.3+
C.2
D.2+
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线y=
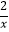 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= 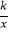 (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 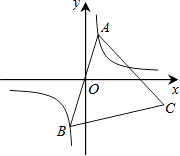
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多
 元,用
元,用 元购得的排球数量与用
元购得的排球数量与用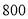 元购得的足球数量相等.
元购得的足球数量相等.⑴排球和足球的单价各是多少元?
⑵若恰好用去
 元,有哪几种购买方案?
元,有哪几种购买方案?
相关试题

