【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

参考答案:
【答案】(1)①α=12°,β=6°;②α=18°,β=9°,③α=2β,理由见解析;(2)α=2β-180°
【解析】试题分析:(1)①先根据角的和与差求α的值,根据等腰三角形的两个底角相等及顶角为30°得:∠ADE=∠AED=75°,同理可得:∠ACB=∠B=69°,根据外角性质列式:75°+β=69°+12°,可得β的度数;
②同理可求得:α=54°﹣36°=18°,β=9°;
③设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,分别求出∠ADE和∠B,根据∠ADC=∠B+α列式,可得结论;
(2)α=2β﹣180°,理由是:如图(2),设∠E=x°,则∠DAC=2x°,根据∠ADC=∠B+∠BAD,列式可得结论.
解:(1)①∵∠DAE=30°,
∴∠ADE+∠AED=150°,
∴∠ADE=∠AED=75°,
∵∠BAC=42°,
∴α=42°﹣30°=12°,
∴∠ACB=∠B=![]() =69°,
=69°,
∵∠ADC=∠B+α,
∴75°+β=69°+12°,
β=6°;
故答案为:12°,6°;
②∵∠DAE=36°,
∴∠ADE+∠AED=144°,
∴∠ADE=∠AED=72°,
∵∠BAC=54°,
∴α=54°﹣36°=18°,
∴∠ACB=∠B=![]() =63°,
=63°,
∵∠ADC=∠B+α,
∴72°+β=63°+18°,
β=9°;
故答案为:18°,9°;
③α=2β,理由是:
如图(1),设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB=![]() ,
,
∵∠ADE=∠AED,
∴∠AED=![]() ,
,
∴β+∠ADE=α+∠ABC,
β+![]() =α+
=α+![]() ,
,
∴α=2β;
(2)α=2β﹣180°,理由是:
如图(2),设∠E=x°,则∠DAC=2x°,
∴∠BAC=∠BAD+∠DAC=α+2x°,
∴∠B=∠ACB=![]() ,
,
∵∠ADC=∠B+∠BAD,
∴β﹣x°=![]() +α,
+α,
∴α=2β﹣180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某轮船往返于A、B两地之间,设船在静水中的速度不变,那么,当水的流速增大时,轮船往返一次所用的时间( )
A. 不变 B. 增加 C. 减少 D. 增加,减少都有可能
-
科目: 来源: 题型:
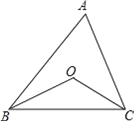
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③
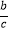 <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 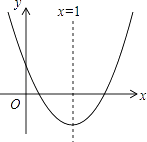
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2
 ,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
A.3
B.3+
C.2
D.2+
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线y=
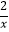 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= 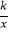 (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 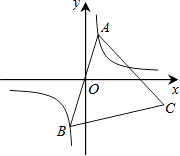
相关试题

