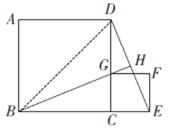
【题目】已知,如图所示,正方形![]() 的边长为1,
的边长为1,![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 与
与![]() 、
、![]() 不重合),以
不重合),以![]() 为一边向正方形
为一边向正方形![]() 外作正方形
外作正方形![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:①![]() ≌△
≌△![]() . ②
. ②![]() .
.
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长.
的长.
参考答案:
【答案】(1)①见详解;②见详解;(2)![]()
【解析】
①根据正方形确定BC=DC,CE=CG及∠BCD=∠ECG=900,即可证明全等;
②根据(1)的全等得出∠BGC=∠DEC,再根据∠BGC+∠CBG=900,即可证得![]()
(2)根据勾股定理求出线段BD的长,然后利用三角形全等证出BE=BD,再由BE-BC求出CE即CG的长.
(1)①∵四边形![]() 与四边形
与四边形![]() 均为正方形,
均为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=900,
∴![]() ≌△
≌△![]()
②∵![]() ≌△
≌△![]() ,
,
∴∠BGC=∠DEC,
∵∠BGC+∠CBG=900,
∴∠DEC+∠CGB=900
∴∠BHE=900
即![]()
(2) 连接BD,
∵四边形ABCD是正方形,边长为1,
∴AB=AD=1,∠A=900,
∴![]()
![]()
∵BH平分DE,BH⊥DE,
∴DH=EH,∠BHD=∠BHE,
又∵BH=BH
∴△BHD≌△BHE,
∴BE=BD=![]() ,
,
∴CG=CE=BE-BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的中点
的中点①用直尺和圆规在
 边上求作点
边上求作点 ,使得
,使得 (保留作图痕迹,不要求写作法);
(保留作图痕迹,不要求写作法);②在①的条件下,如果
 ,那么
,那么 是
是 的中点吗?为什么?
的中点吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.

(1)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段AE与EF又有怎样的数量关系?请直接写出你的猜想,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校未了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按
 ,
, ,
, ,
, 四个等级进行统计,制成了如下不完整的统计图.
四个等级进行统计,制成了如下不完整的统计图. 
根据所给信息,解答以下问题
(1)在扇形统计图中,
 对应的扇形的圆心角是________度;
对应的扇形的圆心角是________度;(2)补全条形统计图;
(3)该校九年级有300名学生,请估计足球运球测试成绩达到
 级的学生有多少人?
级的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知
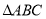 中,
中,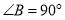 ,
,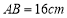 ,
,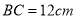 ,
,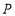 、
、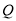 是
是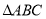 边上的两个动点,其中点
边上的两个动点,其中点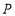 从点
从点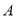 开始沿
开始沿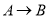 方向运动,且速度为每秒
方向运动,且速度为每秒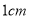 ,点
,点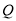 从点
从点 开始沿
开始沿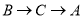 方向运动,且速度为每秒
方向运动,且速度为每秒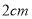 ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为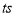 .
. 
(1)出发
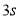 后,求
后,求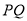 的长;
的长;(2)当点
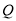 在边
在边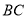 上运动时,出发多久后,
上运动时,出发多久后,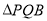 能形成等腰三角形?
能形成等腰三角形?(3)当点
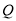 在边
在边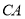 上运动时,求能使
上运动时,求能使 成为等腰三角形的运动时间.
成为等腰三角形的运动时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC与△CDE都是等边三角形,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AFB=60°;③BF=AH;④△ECF≌△DCG;⑤连CG,则∠BGC=∠DGC.其中正确的个数是()

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠C=90°,AC=BC=7,D是AB的中点,点E在AC上,点F在BC上,DE=DF,若BF=4,则EF=_______
相关试题

