Question

【题目】如图，在中，为的中点

①用直尺和圆规在边上求作点，使得(保留作图痕迹，不要求写作法)；

②在①的条件下，如果，那么是的中点吗？为什么？

Answer 1

【答案】①作图见详解，②Q是GN的中点，证明见详解.

【解析】

①利用尺规进行作图即可，注意要保留作图痕迹.

②证明是的中点，根据①的条件大胆猜想综合运用等角和等边转换，从而分析证明.

解：①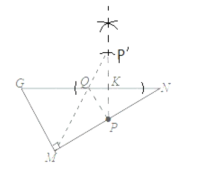

② 在①的条件下，如果∠G=60°，那么Q是GN的中点，理由如下：

设PP'交GN于点K，

∵∠G=60°，∠GMN=90°，

∴∠N=90°─60°=30°，

∵点P关于GN的对称点是点P'，

∴PK⊥KN，PK=P P'，

∴∠PKN=90°，又∵∠N=30°，

∴PK=PN，PP'=PN，

∵P为MN的中点，

∴PM=PN，PP'=PM，

∴∠PР'M=∠PMР'，

∵∠PK N=90°，∠N=30°，

∴∠NРK=90°-30°=60°，

又∵∠PP'M+∠PMP’=∠NPK，

∴∠PM P'=×60°=30°，又∵∠N=30°，

∴∠PM P'=∠N，QM=QN，

∵∠GMN=90°，∠PM P'=30°，

∴∠GMQ=90°-30°=60°，

又∵∠G=60°，

∴∠GMQ=∠G，

∴QG=QM，又∵QM=QN，

∴QG=QN，Q是GN的中点。