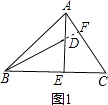
【题目】如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
参考答案:
【答案】
(1)
解:BD=AC,BD⊥AC,
理由:延长BD交AC于F.
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在△BED和△AEC中 
∴△BED≌△AEC,
∴BD=AC,∠DBE=∠CAE,
∵∠BED=90°,
∴∠EBD+∠BDE=90°,
∵∠BDE=∠ADF,
∴∠ADF+∠CAE=90°,
∴∠AFD=180°﹣90°=90°,
∴BD⊥AC
(2)
解:
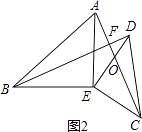
不发生变化,
理由是:∵∠BEA=∠DEC=90°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中 
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°﹣90°=90°,
∴BD⊥AC
(3)
解:能.
理由:∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中中 
∴△BED≌△AEC,
∴∠BDE=∠ACE,
∴∠DFC=180°﹣(∠BDE+∠EDC+∠DCF)
=180°﹣(∠ACE+∠EDC+∠DCF)
=180°﹣(60°+60°)
=60°,
即BD与AC所成的角的度数为60°或120°
【解析】(1)延长BD交AC于F,求出∠AEB=∠AEC=90°,证出△BED≌△AEC,推出BD=AC,∠DBE=∠CAE,根据∠EBD+∠BDE=90°推出∠ADF+∠CAE=90°,求出∠AFD=90°即可;(2)求出∠BED=∠AEC,证出△BED≌△AEC,推出BD=AC,∠BDE=∠ACE,根据∠ACE+∠EOC=90°求出∠BDE+∠DOF=90°,求出∠DFO=90°即可;(3)求出∠BED=∠AEC,证出△BED≌△AEC,推出∠BDE=∠ACE,根据三角形内角和定理求出∠DFC即可.
【考点精析】掌握三角形的内角和外角和全等三角形的性质是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A.三点确定一个圆
B.平分弦的直径垂直于弦
C.圆有无数条对称轴,任何一条直径都是它的对称轴
D.同弧或等弧所对圆心角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长的关系是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明:
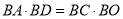 ;
;(3)若AC=5,BC=12,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个有理数﹣2,1,0,﹣1,其中最小的数是( )
A. 1B. 0C. ﹣1D. ﹣2
-
科目: 来源: 题型:
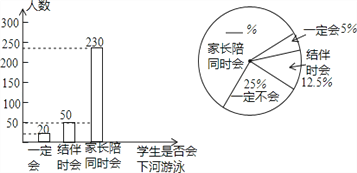
查看答案和解析>>【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 名学生;
(2)“家长陪同时会”的学生所占比例为 %,“一定不会”的学生有 人;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体从前面看及从上面看的视图如图所示。这样的几何体只有一种吗?它最多要多少个小立方体?最少要多少个小立方体?


相关试题

