【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
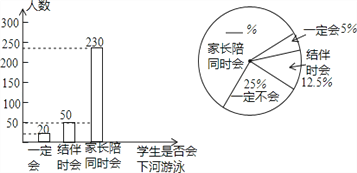
(1)这次抽样调查中,共调查了 名学生;
(2)“家长陪同时会”的学生所占比例为 %,“一定不会”的学生有 人;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
参考答案:
【答案】解:(1)400。
(2)一定不会的人数是400﹣20﹣50﹣230=100(人),
家长陪同的所占的百分比是![]() ×100%=57.5%。
×100%=57.5%。
补图如下:
(3)根据题意得:2000×5%=100(人)。
答:该校2000名学生中大约有多少人“一定会下河游泳”有100人。
【解析】(1)根据一定会的人数和所占的百分比即可求出总人数:20÷5%=400(人)。
(2)用总人数减去其它人数得出不会的人数,再根据家长陪同的人数除以总人数得出家长陪同时会的所占的百分比,从而补全统计图。
(3)用2000乘以一定会下河游泳所占的百分百,即可求出该校一定会下河游泳的人数。
-
科目: 来源: 题型:
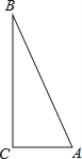
查看答案和解析>>【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明:
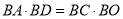 ;
;(3)若AC=5,BC=12,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.

(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个有理数﹣2,1,0,﹣1,其中最小的数是( )
A. 1B. 0C. ﹣1D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体从前面看及从上面看的视图如图所示。这样的几何体只有一种吗?它最多要多少个小立方体?最少要多少个小立方体?


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中确定事件是( )
A.掷一枚均匀的硬币,正面朝上
B.买一注福利彩票一定会中奖
C.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球
D.掷一枚六个面分别标有,1,2,3,4,5,6的均匀正方体骰子,骰子停止转动后奇数点朝上
-
科目: 来源: 题型:
查看答案和解析>>【题目】4a-a的计算结果是( )
A. 3 B. 3a C. 4 D. 4a
相关试题

