【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明: ![]() ;
;
(3)若AC=5,BC=12,求⊙O的半径.
参考答案:
【答案】实践操作:作图见解析;
综合运用:(1)相切;(2)证明见解析;(3)⊙O的半径为![]() .
.
【解析】试题分析:(1)、根据角平分线的性质得出OC=OD,从而得出圆与直线的位置关系;(2)、根据相切的性质以及公共角得出△ABC和△OBD相似,从而得出答案;(3)、根据题意得出AD=AC=5,AB=13,则BD=8,设半径为x,则OB=12-x,根据Rt△BOD的勾股定理求出x的值,得出圆的半径.
试题解析:实践操作,如图所示:
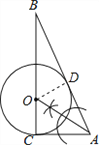
综合运用:
(1)相切
(2)因为∠BCA=90°,∠BDO=90°, 所以△ABC∽△OBD;
所以![]() 即
即![]() .
.
(3)因为AC=5,BC=12, 所以AD=5,AB=13, 所以DB=13﹣5=8,
设半径为x ,则OC=OD=x ,BO=(12﹣x), x2+82=(12﹣x)2,
解得:x=![]() .答:⊙O的半径为
.答:⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E为等腰△ABC的底边BC上一动点,过E作EF⊥BC交AB于D,交CA的延长线于F,问:
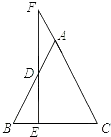
(1)∠F与∠ADF的关系怎样?说明理由;
(2)若E在BC延长线上,其余条件不变,上题的结论是否成立?若不成立,说明理由;若成立,画出图形并给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A.三点确定一个圆
B.平分弦的直径垂直于弦
C.圆有无数条对称轴,任何一条直径都是它的对称轴
D.同弧或等弧所对圆心角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长的关系是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.

(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个有理数﹣2,1,0,﹣1,其中最小的数是( )
A. 1B. 0C. ﹣1D. ﹣2
-
科目: 来源: 题型:
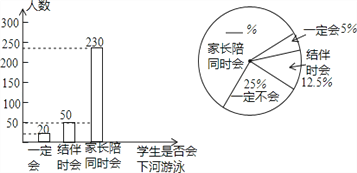
查看答案和解析>>【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 名学生;
(2)“家长陪同时会”的学生所占比例为 %,“一定不会”的学生有 人;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
相关试题

