【题目】如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
求证:DB=DC.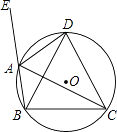
参考答案:
【答案】证明:∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC.
∵AD平分∠CAE,
∴∠EAD=∠DAC,
∴∠EAD=∠DBC.
∵四边形ABCD内接于⊙O,
∴∠EAD=∠BCD,
∴∠DBC=∠DCB,
∴DB=DC
【解析】先根据圆周角定理得出∠DAC=∠DBC,再由角平分线的性质得出∠EAD=∠DAC,根据圆内接四边形的性质得出∠EAD=∠BCD,由此可得出结论.
【考点精析】利用圆周角定理和圆内接四边形的性质对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.
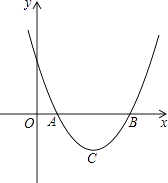
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
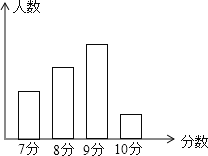
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中, 直角三角形的个数为
①
 ②
②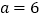 ,∠A=45°;③∠A=32°, ∠B=58°;
,∠A=45°;③∠A=32°, ∠B=58°;④
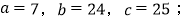 ⑤
⑤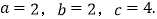 ⑥
⑥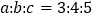
⑦
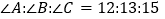 ⑹
⑹
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距学校6km的郊外游玩,一部分同学步行,另一部分同学骑车。如图,
 分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是
分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是 
A. 骑车的同学比步行的同学晚出发30min
B. 步行的同学的速度是6km/h
C. 骑车的同学从出发到追上步行的同学用了20min
D. 骑车的同学和步行的同学同时到达目的地
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射靶
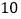 次,将射击结果作统计分析如下:
次,将射击结果作统计分析如下:命中环数
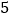
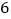
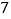
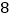
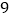
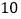
平均数
众数
方差
甲命中环数的次数
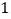
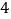
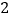
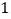
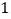
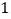
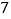
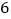
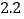
乙命中环数的次数
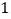
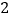
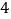
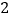
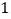
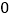
________
________
________
 请你完成上表中乙进行射击练习的相关数据;
请你完成上表中乙进行射击练习的相关数据; 根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.
根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

相关试题

