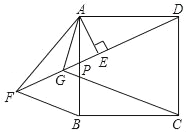
【题目】如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=![]() DG.
DG.
参考答案:
【答案】证明见解析
【解析】试题分析:(1)根据线段垂直平分线的定义得到AF=AD,根据等腰三角形的性质、角平分线的定义证明即可;
(2)作CH⊥DP,交DP于H点,证明△ADE≌△DCH(AAS),得到CH=DE,DH=AE=EG,证明CG=![]() GH,AG=
GH,AG=![]() DH,计算即可.
DH,计算即可.
试题解析:
(1)证明:∵DE=EF,AE⊥DP,
∴AF=AD,
∴∠AFD=∠ADF,
∵∠ADF+∠DAE=∠PAE+∠DAE=90°,
∴∠AFD=∠PAE,
∵AG平分∠BAF,
∴∠FAG=∠GAP.
∵∠AFD+∠FAE=90°,
∴∠AFD+∠PAE+∠FAP=90°
∴2∠GAP+2∠PAE=90°,
即∠GAE=45°,
∴△AGE为等腰直角三角形;
(2)证明:作CH⊥DP,交DP于H点,
∴∠DHC=90°.
∵AE⊥DP,
∴∠AED=90°,
∴∠AED=∠DHC.
∵∠ADE+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠ADE=∠DCH.
∵在△ADE和△DCH中,
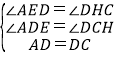 ,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=EG.
∴EH+EG=EH+HD,
即GH=ED,
∴GH=CH.
∴CG=GH.
∵AG=![]() EG,
EG,
∴AG=![]() DH,
DH,
∴CG+AG=![]() GH+
GH+![]() HD,
HD,
∴CG+AG=![]() (GH+HD),
(GH+HD),
即CG+AG=![]() DG.
DG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x+y,B=2x﹣y,计算A2﹣B2 .
-
科目: 来源: 题型:
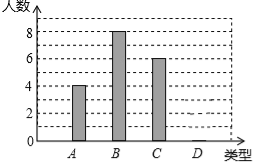
查看答案和解析>>【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=--
 x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

-
科目: 来源: 题型:
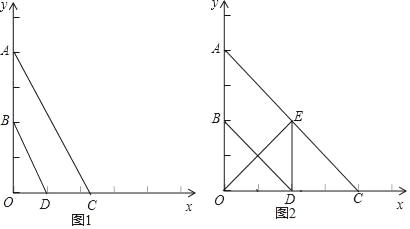
查看答案和解析>>【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a﹣a,正确的结果是( )
A.﹣2a3
B.1
C.2
D.a
相关试题

