搜索
【题目】如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形OCED的周长为（ ）
A. 4 B. 8 C. 10 D. 12
参考答案：
【答案】B
【解析】由四边形ABCD为矩形，得到OD=OC，再利用平行四边形的判定得到四边形DECO为平行四边形，利用菱形的判定定理得到四边形DECO为菱形，根据AC的长求出OC的长，即可确定出其周长．
解：∵四边形ABCD为矩形，
∴OA=OC，OB=OD，且AC=BD，
∴OA=OB=OC=OD=2，
∵CE∥BD，DE∥AC，
∴四边形DECO为平行四边形，
∵OD=OC，
∴四边形DECO为菱形，
∴OD=DE=EC=OC=2，
则四边形OCED的周长为2+2+2+2=8，
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=--
x＋8与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．(1)求AB的长和点C的坐标；
(2)求直线CD的表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，P为AB边上任意一点，AE⊥DP于E，点F在DP的延长线上，且EF=DE，连接AF、BF，∠BAF的平分线交DF于G，连接GC．
（1）求证：△AEG是等腰直角三角形；
（2）求证：AG+CG=
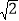DG．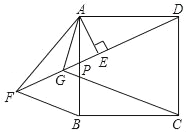
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，平面直角坐标系中，A（0，4），B（0，2），点C是x轴上一点，点D为OC的中点．
（1）求证：BD∥AC；
（2）若点C在x轴正半轴上，且BD与AC的距离等于1，求点C的坐标；
（3）如果OE⊥AC于点E，当四边形ABDE为平行四边形时，求直线AC的解析式．
-
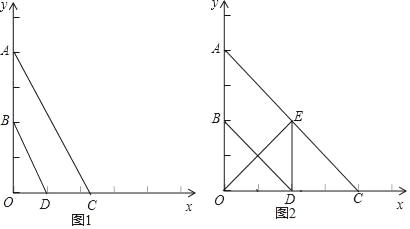
科目： 来源： 题型：
查看答案和解析>>【题目】计算2a﹣a，正确的结果是（ ）
A.﹣2a3
B.1
C.2
D.a -
科目： 来源： 题型：
查看答案和解析>>【题目】若a和b都是有理数，则下列①若a≠b，则a2≠b2；②若a＞b，则a2＞b2；③若a＞b，则|a|＞|b|；④若a2＞b2 ， 则a＞b说法中，正确的个数是（ ）
A.0个
B.1个
C.2个
D.3个 -
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习了正方形之后，给同桌小文出了错题，从下列四个条件：
①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使ABCD为正方形（如图所示），现有如下四种选法，你认为其中错误的是（ ）
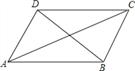
A. ①② B. ①③ C. ②③ D. ②④
相关试题
