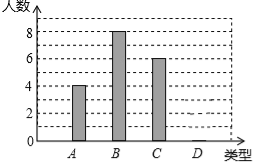
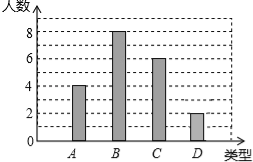
【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
参考答案:
【答案】(1)图形见解析
(2)众数为5,中位数是5;
(3)估计这240名学生共植树1272棵.
【解析】试题分析:(1)先求出D类的人数,然后补全统计图即可;
(2)由众数的定义解答,根据中位数的定义,因为是20个人,因此找出第10人和第11人植树的棵树,求出平均数即为中位数;
(3)求出20人植树的平均棵树,然后乘以总人数240计算即可得解.
试题解析:(1)D类的人数为:20﹣4﹣8﹣6=20﹣18=2人,
补全统计图如图所示;
(2)由图可知,植树5棵的人数最多,是8人,
所以,众数为5,
按照植树的棵树从少到多排列,第10人与第11人都是植5棵数,
所以,中位数是5;
(3)![]() =5.3(棵),
=5.3(棵),
240×5.3=1272(棵).
答:估计这240名学生共植树1272棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与直线y=2x+3交于点M(0,3), A(a,15).点B是抛物线上M,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线MA交于点C,E.以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),请写出m,n之间的关系式________________ .
与直线y=2x+3交于点M(0,3), A(a,15).点B是抛物线上M,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线MA交于点C,E.以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),请写出m,n之间的关系式________________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x+y,B=2x﹣y,计算A2﹣B2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=--
 x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=
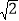 DG.
DG.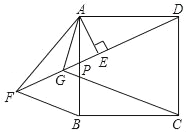
-
科目: 来源: 题型:
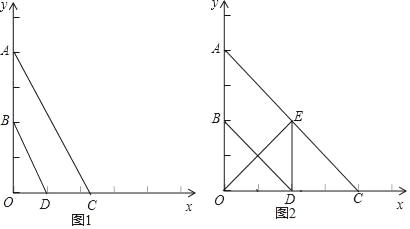
查看答案和解析>>【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
相关试题

