【题目】如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为( ) 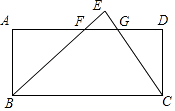
A.1
B.![]()
C.![]()
D.2
参考答案:
【答案】C
【解析】解:∵四边形ABCD是矩形, ∴AB=CD,AD=BC=6,∠A=∠D=90°,
∵∠E=90°,
∴∠EFG+∠EGF=90°,
∴∠AFB+∠DGC=90°,
∵∠AFB+∠ABF=90°,
∴∠ABF=∠DGC,
∴△AFB∽△DCG,
∴ ![]() ,
,
∵AF:FG:GD=3:2:1,
∴AF=3,DG=1,
∴AB2=AFDG=3,
∴AB= ![]() .
.
故选C.
【考点精析】掌握矩形的性质和相似三角形的判定与性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
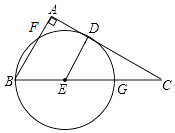
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D为BC边上一点.

(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4 ,BC=6,∠B=45°,则CD的取值范围是 .
,BC=6,∠B=45°,则CD的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术饰品
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内接于⊙O,E是
 的中点,连接BE、CE,则∠ABE=°.
的中点,连接BE、CE,则∠ABE=°. 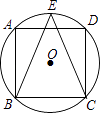
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习过反比例函数y=
 的图象和性质,请回顾研究它的过程,对函数y=
的图象和性质,请回顾研究它的过程,对函数y=  进行探索.下列结论:
进行探索.下列结论:
①图象在第一、二象限,②图象在第一、三象限,
③图象关于y轴对称,④图象关于原点对称,
⑤当x>0时,y随x增大而增大;当x<0时,y随x增大而增大,
⑥当x>0时,y随x增大而减小;当x<0时,y随x增大而增大,
是函数y= 的性质及它的图象特征的是: . (填写所有正确答案的序号)
的性质及它的图象特征的是: . (填写所有正确答案的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,CA=4,CB=3.
 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 .
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 . 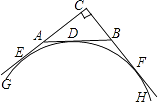
相关试题

