【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G. 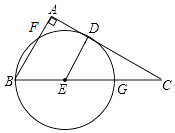
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= .
参考答案:
【答案】
(1)证明:∵CDBC=ACCE,
∴ ![]() ,
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线
(2)①如图1,
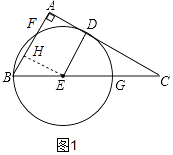
过E作EH⊥AB于H,
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH﹣AF=DE﹣AF=r﹣4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴ ![]() ,即
,即 ![]() ,
,
∴r=20,
∴⊙E的半径为20
(3)![]()
【解析】如图2 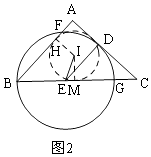
过I作IM⊥BC于M,过I作IH⊥AB于H,
由(2)得:FH=BH=r﹣4=20﹣4=16,AB=AF+2BH=4+2×16=36,
BC=2r+5=2×20+5=45,
∴AC= ![]() =27,
=27,
∵I是Rt△ABC的内心,
∴IM= ![]() =
= ![]() =9,
=9,
∴AH=IM=9,
∴BH=BM=36﹣9=27,
∴EM=27﹣20=7,
在Rt△IME中,由勾股定理得:IE= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了等腰直角三角形和三角形的内切圆与内心的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元? -
科目: 来源: 题型:
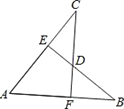
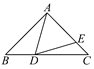
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠BAC=90°,∠BAD=30°,AD=AE,则∠EDC的度数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D为BC边上一点.

(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4 ,BC=6,∠B=45°,则CD的取值范围是 .
,BC=6,∠B=45°,则CD的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术饰品
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
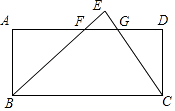
查看答案和解析>>【题目】如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为( )
A.1
B.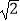
C.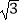
D.2
相关试题

