【题目】如图,在△ABC中,∠C=90°,CA=4,CB=3. ![]() 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 .
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 . 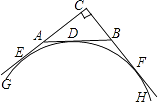
参考答案:
【答案】6
【解析】解: 在Rt△ACB中,∠C=90°,AC=,BC=3,由勾股定理得:AB=5,
设弧所在的圆的圆心为O,圆的半径为r,连接OE、OF,如图,
∵. ![]() 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,
∴AE=AD,BF=BD,∠OEC=∠OFC=90°,
∵∠C=90°,OE=OF=r,
∴四边形CEOF是正方形,
∴CE=CF=OE=OF=r,
则AE=AD=r﹣4,BF=DB=r﹣3,
∴r﹣3+r﹣4=5,
解得:r=6,
所以答案是:6.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为( )
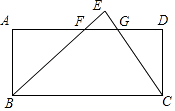
A.1
B.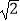
C.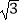
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内接于⊙O,E是
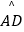 的中点,连接BE、CE,则∠ABE=°.
的中点,连接BE、CE,则∠ABE=°. 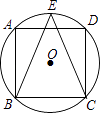
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习过反比例函数y=
 的图象和性质,请回顾研究它的过程,对函数y=
的图象和性质,请回顾研究它的过程,对函数y=  进行探索.下列结论:
进行探索.下列结论:
①图象在第一、二象限,②图象在第一、三象限,
③图象关于y轴对称,④图象关于原点对称,
⑤当x>0时,y随x增大而增大;当x<0时,y随x增大而增大,
⑥当x>0时,y随x增大而减小;当x<0时,y随x增大而增大,
是函数y= 的性质及它的图象特征的是: . (填写所有正确答案的序号)
的性质及它的图象特征的是: . (填写所有正确答案的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为x厘米/秒,则当△BPD与△CQP全等时,x的值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接DE并延长至点F,使EF=DE,连接AF、DC.求证:四边形ADCF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
相关试题

