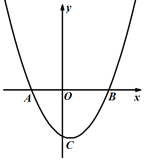
【题目】如图,抛物线![]() 分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .
分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .
(1)求点A,B的坐标.
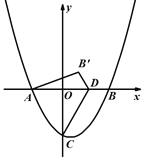
(2)当点B′落坐标轴上时,求点D的坐标.
(3)在点D的运动过程中,△AB′D 的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
参考答案:
【答案】(1)A(-2,0) , B(3,0) (2)B’在以C为圆心,CB为半径的圆C上;(3)① ![]() ②(
②(![]() )③(
)③(![]() )
)
【解析】分析:(1)令y=0,可求得x的值,从而可确定A、B两点坐标;
(2)分两种情况进行讨论:①当B’点落在x轴上,②当B’点落在y轴上,利用对称性求解即可;
(3)如图,分三种情况进行求解.
详解(1)由y=0解得x1=-2,x2=3,
∴ A(-2,0) , B(3,0)
(2)B’在以C为圆心,CB为半径的圆C上;
①当B’点落在x轴上时,D(0,0);
②当B’点落在y轴上时,如图1,CB’=CB=![]() ,
,
∵∠OB’D=45°
∴OD=OB’=![]() -3
-3
∴ D(![]() )
)
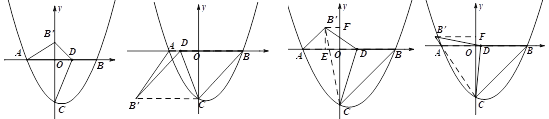
图1 图2 图3 图4
(3)①∠B’DA=45°时,如图1,OB’=![]() -3,B’(0,
-3,B’(0,![]() -3).
-3).
如图2,连接CB’,∠B’DA=∠CBD=45°,∴DB’∥BC,可得四边形DB’CB是菱形,B’(-![]() -3).
-3).
②∠B’AD=45°如图3,连接CB’,过点B’分别作坐标轴的垂线,垂足为E、F,设线段FB’的长为m,B’E=AE=2-m,可得CF=5-m,在直角三角形CFB’中,![]() ,解得
,解得![]() ,B’(
,B’(![]() ,
,![]() ).
).
③如图4,∠AB’D=45°,连接CB’,过点B’作Y轴的垂线,垂足为点F,由轴对称性质可得,∠CB’D=∠CBD=45°,所以当∠AB’D=45°时,点A在线段CB’上,所以![]() ,设线段FB’的长为2m,FC=3m,
,设线段FB’的长为2m,FC=3m,![]() ,解得:
,解得:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若∠B=30°,BC=4
 ,求四边形AEDF的周长.
,求四边形AEDF的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一条长度为 a 的线段.
(1)如图①,以该线段为直径画一个圆,该圆的周长 C1 = ;如图②,分别以该线段的一半为直 径画两个圆,这两个圆的周长的和 C2 = (都用含 a 的代数式表示,结果保留 )
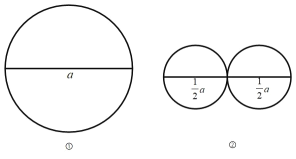
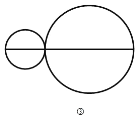
(2)如图③,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为 C3 ,探索 C1 和 C3 的数量关系,并说明理由。
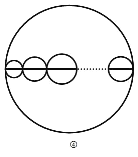
(3)如图④,当 a =10 时,以该线段为直径画一个大圆,再在大圆内画若干个小圆,这些小圆的直径都和 大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有圆的周长的和为 (结 果保留 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,1),B(0,
 ),C(3,0).
),C(3,0).
(1)若以A、B、C、D为顶点的四边形是平行四边形,则请你写出所有符合条件的D点坐标.
(2)直接写出一个符合(1)中条件的直线AD 的解析式.
(3)求平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式
 ,
, 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
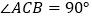 ,
,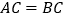 ,
,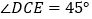 ,如果
,如果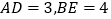 ,则
,则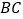 的长是( ).
的长是( ).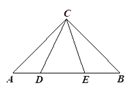
A.
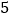 B.
B. 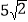 C.
C. 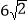 D.
D. 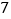
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区为了解居民对居住环境的满意度情况(满意度分为四个等级:
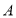 、非常满意:
、非常满意: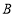 、满意;
、满意; 、基本满息;
、基本满息;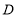 、不满意),在某小区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.
、不满意),在某小区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.
请你结合图中提供的信息解答下列问题.
(1)这次被调查的居民共有______户,并将条形统计图补充完整.
(2)请计算扇形统计图中
 所在扇形的圆心角度数.
所在扇形的圆心角度数.(3)若该小区有2500户居民,请你估计这个小区大约有多少户居民对居住环境的满意度是“非常满意”.
相关试题

