【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC= ![]() ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC= ![]() 中正确的有( )
中正确的有( )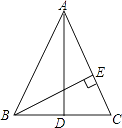
A.①②
B.②③
C.①②③
D.①②③④
参考答案:
【答案】A
【解析】解:∵AD⊥BC垂足为点D,AD是BC边上的中线,
∴AD垂直平分BC,
∴AB=AC,∴①正确;
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD= ![]() ∠BAC,
∠BAC,
∵BE⊥AC,AD⊥BC,
∴∠EBC+∠C=90°,∠DAC+∠C=90°,
∴∠EBC=∠DAC,
∴∠EBC= ![]() ∠BAC,∴②正确;
∠BAC,∴②正确;
∵AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , AB≠BC,
∴AE≠CE,∴③错误;
∵∠BAC≠∠ABC,∠EBC= ![]() ∠BAC,
∠BAC,
∴∠EBC≠ ![]() ∠ABC,∴④错误;
∠ABC,∴④错误;
∴①②都正确;
故答案为:A.
由题知AD垂直平分BC,根据垂直平分线上的点到角两边的距离相等得出AB=AC ;根据等腰三角形的三线合一得出∠BAD=∠CAD= ![]() ∠BAC,然后又根据同角的余角相等得出∠EBC=∠DAC,通过等量代换得出∠EBC=
∠BAC,然后又根据同角的余角相等得出∠EBC=∠DAC,通过等量代换得出∠EBC= ![]() ∠BAC ;根据勾股定理得出AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , 又AB≠BC,从而得出AE≠CE ;根据∠BAC≠∠ABC,∠EBC=
∠BAC ;根据勾股定理得出AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , 又AB≠BC,从而得出AE≠CE ;根据∠BAC≠∠ABC,∠EBC= ![]() ∠BAC,从而得出∠EBC≠
∠BAC,从而得出∠EBC≠ ![]() ∠ABC 。
∠ABC 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
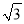 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在我市双城同创的工作中,某社区计划对1200m2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
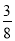 ,cos22°≈
,cos22°≈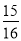 ,tan22≈
,tan22≈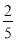 )
) -
科目: 来源: 题型:
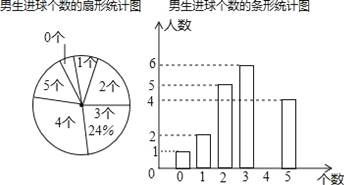
查看答案和解析>>【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个)
人数
0
1
1
2
2
x
3
y
4
4
5
2
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.
相关试题

