【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元?
参考答案:
【答案】
(1)解:设A种商品销售x 件,
则B种商品销售(100-x)件.
依题意,得 10x+15(100-x)=1350
解得x=30.
∴100-x=70.
答:A种商品销售30件,B种商品销售70件
(2)解:设购进A种商品m件,则购进B商品(200-m)件,根据题意的
0≤200-m≤3m
解之:200≤m≤50
设所获利润为W元,根据题意得
w=10m+15(200-m)=-5m+3000
∵-5<0.
∴w随m的增大而减小,
∴当m=50时,所得利润最大
∴w=-5×50+3000=2750
200-m=150
答:为了获得最大利润,应购进A商品50件,应购进B商品150件,可获得最大利润为2750元。
【解析】(1)此题等量关系是:A商品的件数+B商品=100;每件A商品的利润![]() A商品的数量+每件B商品的利润
A商品的数量+每件B商品的利润![]() B商品的数量=1350;建立方程或出租。求解即可。
B商品的数量=1350;建立方程或出租。求解即可。
(2)根据题意可得不等关系:0≤B种商品的件数≤3![]() A种商品件数,建立不等式组求解即可;设所获利润为W元,得出w=每件A商品的利润
A种商品件数,建立不等式组求解即可;设所获利润为W元,得出w=每件A商品的利润![]() A商品的数量+每件B商品的利润
A商品的数量+每件B商品的利润![]() B商品的数量,建立函数解析式,再根据一次函数的性质求出结果即可。
B商品的数量,建立函数解析式,再根据一次函数的性质求出结果即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种原子质量为0.00001992g,用科学记数法表示为______g.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
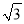 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=
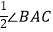 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC= 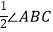 中正确的有( )
中正确的有( )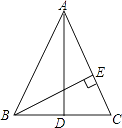
A.①②
B.②③
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在我市双城同创的工作中,某社区计划对1200m2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
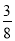 ,cos22°≈
,cos22°≈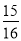 ,tan22≈
,tan22≈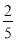 )
)
相关试题

